Plotly.js: Mesh3d does not reproduce scatter3d - alphahull issue?

[PhilW1952]

I am trying to put two plots on div, one a mesh3d and one a scatter3d.
The function psi is a spherical harmonic Y21 (r, theta, phi) plotted on a a sphere whose radius r (for each x,y,z point) depends on the value of the function Y.

The results are at https://codepen.io/PhilW/pen/ZovmjE.

I have two issues.

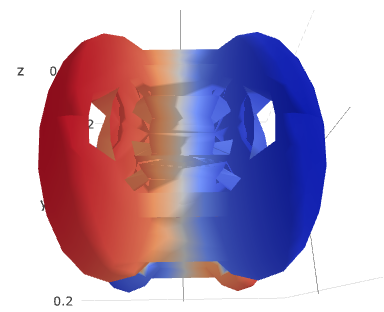
The first is that the mesh3d plot on the right does not match the scatter3d on the left. The scatter3d plot correctly show the 4 lobes of the function (spin it to see this better). But the mesh3d plot, for the same data, show a weird box shape. It does show colors in the correct places (red = pos, blue = neg) but the surface generated is not correct. I have tried various values of alphahull, positive values help a little. The docs suggest that it is best to supply i,j,k indices, but I don't know how to easily do this from my x,y,z vertices. Other routines seem to do these sort of plots easily (MathLab) or have specific routines to generate indices (Three). If I force r =1 the mesh3d draws a sphere that has intensity colors at the correct places corresponding to the values of psi. What am I missing?

The second problem is weird. The codepen uses a a newPlot(trace1) followed by an addTraces(trace2). This works fine. But if I changes this to data = [trace1, trace] followed by newPlot(data) the routine crashes displaying a blank 2D graph. You can do this for yourself by changing the // at the end. This seems crazy!

[PhilW1952]

You can ignore the second problem. I had written trace1 = [{ ... }] instead of trace1 = { ... }!
But the alphahull issue is real.

[etpinard]

If you don't want to construct vertices, I suggest trying to plot spherical harmonics as type: 'surface' traces with 2D x, y and z arrays.

See an example:

https://plot.ly/~empet/13990/spherical-voronoi-diagram.embed

With its corresponding json: https://plot.ly/~empet/13990/spherical-voronoi-diagram.json

[alexcjohnson]

@etpinard's suggestion is probably the right way to handle this - you may find this reference useful: https://plot.ly/python/3d-parametric-plots/ (in Python but it translates easily to JS)

But it's interesting that alphahull doesn't work in this seemingly fairly simple case - as you say, positive values help a little, up to about 5 you can start to see the shape emerge but above that any more detail is mooted by the appearance of unwanted holes. I wonder if there would be some smarter variant of the alphahull algorithm, that determines a dynamic connection radius based on the local density of points or something?

It's also quite possible we have a bug in that algorithm at the moment. For example here's your plot at alphahull: 5 - why would it connect that pane across the bottom, then leave a gap? Seems weird.

And increasing to alphahull: 6, gaps open up that look to be substantially smaller than connections that we do draw from lobe to lobe, which I wouldn't have expected.

[PhilW1952]

Etienne/Alex - Thank you for the fast replies!

I have used surface in the past with a 1D x, 1D y and 2D z array and it worked fine. Is that what you meant? I see that the sphere JSON appears to have multiple arrays inside x , y and z. I am a little confused how to get from my set of 1D xyz coords to a form that surface likes. If I send my present data (as the Python example seems to do) straight to surface it crashes.

[alexcjohnson]

right, it needs to be 2D arrays, of the same shape, for all 3 arrays. You've already got a 2D loop, just use both indices as the array indices https://codepen.io/alexcjohnson/pen/NMyOmg

(also needed to change intensity to surfacecolor)

[PhilW1952]

I have a general question for you experts. When is it best to use mesh vs surface? I expected that surface would work best for a function that does not enclose space, whereas mesh would be best for e.g. a sphere. Yet surface seems to work for a sphere. Do surface and mesh treat connecting points to make a surface in different ways? Phil

[PhilW1952]

Alex - that is fantastic, thanks for the help. Also, I didn't know that you could say x = x2 = something (I am coming from FORTRAN/VB)

[alexcjohnson]

If you can parametrize it, use surface. That way it's clear on the level of the data structures which points are supposed to be connected to which other points.

If you have a surface with more complicated topology, or the data are just a collection of arbitrary (x,y,z) triplets, you need to use mesh3d - but the caveat is that if you don't provide the connections yourself (i, j, k vertex arrays to define the triangles) we'll have to guess. With the exception of data that are single-valued in one of the axes (so you can use Delaunay triangulation - for example you know z is a function of x and y but you have irregularly arranged data points) our algorithms for this obviously leave something to be desired.

@etpinard do you want to leave this open for someone to look at whether alphahull is really doing the right thing and/or if another algorithm could do better? Or would you prefer to close this as too speculative / distant a concern?

[etpinard]

I'm no simplicial complex expert, but as far as I know, supplying only x/y/z in a mesh3d trace is asking for trouble. So, I'd vote for closing this issue.

[alexcjohnson]

Again, I think the Delaunay case is an exception to that, but sounds good - closing until we hit a more problematic or clear-cut case.