Three.js: Feature request: uniform random rotation sampling

[cdalizadeh]

I'd like to be able to apply a random rotation to an object. There are a couple of ways I initially thought to do this: random euler angles, random (normalized) rotation matrix values, and random (normalized) quaternion values.

The problem is, none of these random rotation methods sample uniformly from SO(3), the set of all 3D rotations. From the (admittedly, limited) research I've done, it appears that there are two methods that do sample uniformly from SO(3):

1. Generate a random point along the surface of a unit sphere, convert the point to a vector, and combine the vector with a random rotation 0 < u < 2*PI to form an axis-angle rotation representation. For generating a random point on the surface of a unit sphere, see the following: https://mathworld.wolfram.com/SpherePointPicking.html

2. Generate a random quaternion. The method described in the link below samples uniformly from SO(3): http://planning.cs.uiuc.edu/node198.html

Method 2 seems easy enough, and I plan to use it in my application.

Reading through some of the discussion in https://github.com/mrdoob/three.js/issues/18996, it seems like this may be a compelling enough use case to either:

1. Add a random method to the quaternion class that implements the logic described in method 2 above, or

2. Add this logic to examples/jsm/math/Sampling.js or examples/jsm/math/Random.js, as discussed in https://github.com/mrdoob/three.js/issues/18996#issuecomment-606243878

What do you all think? I'd understand if you think it's too application-specific, but I figured I'd raise the idea anyway. I'd be happy to write a PR for either solution if you'd like.

All the best,
Cameron

[mrdoob]

@WestLangley We could also add random() to Euler?

    random: function () {

        this._x = Math.random() * Math.PI * 2;
        this._y = Math.random() * Math.PI * 2;
        this._z = Math.random() * Math.PI * 2;

        this._onChangeCallback();

        return this;

    }

[makc]

that would be non-uniform, @mrdoob

[cdalizadeh]

I'll try to find a proper source for this soon, but I believe makc is correct. That method would result in non-uniform sampling of SO(3).

[speigg]

+1. I literally just came across the need for this.

[speigg]

https://demonstrations.wolfram.com/SamplingAUniformlyRandomRotation/

"The orientation of a sphere [...] can be represented by three Euler angles. However, uniformly sampling three Euler angles does not result in a uniform sampling. To generate a _uniformly distributed random rotation_, first perform a random rotation about the z axis, then rotate the z axis to a random position on the sphere. We can use this same method to generate _uniformly distributed perturbations_ by scaling the z axis rotation and deflection by a number less than 1."

A method like this should enable both uniformly random rotations and perturbations:

randomQuaternion: function(poleTwistScale=1,poleSwingScale=1) { /**/ }

[Mugen87]

I suggest to make examples/jsm/math/Random.js and treat it like Unity's Random class. In this way, different routines for generating random data can be added.

Instead of creating random euler angles, I would prefer creating quaternions instead. And then have a method with and without uniform distribution (which is not always necessary). So Random.rotation() and Random.rotationUniform().

[WestLangley]

I doubt most user knows what a "uniform quaternion" is -- and what they think it is, is not correct. It is also incredibly application-specific.

We need a compelling use case. https://github.com/mrdoob/three.js/issues/18996#issuecomment-606243878.

[makc]

@WestLangley they might not know fancy math terms, but they can tell good distribution from shitty distribution at a glance.

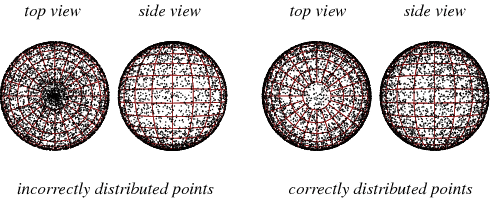
I dont know why are you pushing for simple code instead of the code that produces good results. This is 2nd ticket where you do this now.

[DefinitelyMaybe]

at a guess, it's for all the other people when they look into the code and want to make changes. if the code were complex then making the changes is not so approachable ... for everyone, even the ones that know a bit of math.

[makc]

the change to this code will not be approved any way, because it would increase the complexity.

[speigg]

How is this (too) complicated?

static randomQuaternion = (() => {
    const _2PI = Math.PI * 2;
    const V_001 = new Vector3(0,0,1)
    const twist = new Quaternion
    const swing = new Quaternion
    const swingAxis = new Vector3
    return function randomQuaternion(outQuat, twistScale = 1, swingScale = 1) {
            const twistMagnitude = ( Math.random() - 0.5 ) * _2PI * twistScale 
            const swingDirection = Math.random() * _2PI
            const swingMagnitude = Math.random() * Math.PI * swingScale
            swingAxis.set(1,0,0).applyAxisAngle(V_001, swingDirection)
            twist.setFromAxisAngle(V_001, twistMagnitude)
            swing.setFromAxisAngle(swingAxis, swingMagnitude)
            return outQuat.multiplyQuaternions(swing, twist)
    }
})()