Typescript: OR operator (|) treated like UNION (&) of two types

[selipso]

TypeScript error in /home/thakker/Documents/GitHub/crqcentral/src/Models/helpers.ts(34,64):
Property 'then' does not exist on type 'Promise<GraphQLResult> | Observable<object>'.
  Property 'then' does not exist on type 'Observable<object>'.  TS2339

I've started receiving errors like these too often starting around TypeScript 3.5. They make me feel like pulling my hair out even though I'm already going bald at a young age. Please think about other developers like me in your design decisions before bloating the language even further. I still have fond memories of Typescript 2. Even TypeScript 3.2 was pretty good and then it just kept going downhill from there. It feels like going from Windows XP to Windows Vista.

In the above error, a Promise is clearly listed as a potential return type. Why is TypeScript focusing on the other return type and not inferring that it is a Promise that is being returned based on the syntax of the calling function?

[DanielRosenwasser]

I'm not even sure of the root of the criticism is here - this behavior has been around since TypeScript 1.4 (almost 5 years ago)

The | operator does create a union type, and because the type-checker doesn't know whether you have a Promise or an Observable, it can't be sure whether it's safe to call then.

[dragomirtitian]

Could you post an example of code that worked in earlier versions but not in the latest ? Accessing then on Promise<GraphQLResult> | Observable<object> would never have worked. A union type can be either of the constituents, so you can't access methods that are not common. Consider this simple example:

let o = Math.random() > 0.5 ? 0 : "" // number | string
o.toString() // ok is on both 
o.toExponential() // not ok what if o is string this would be a runtime error
o.toUpperCase()// not ok what if o isnumber  this would be a runtime error

[selipso]

But then what's an appropriate or operator that actually allows you to compose mixed-type functions? And also what's the purpose of duplicating this functionality with &?

[DanielRosenwasser]

&, the intersection type operator.

[selipso]

FYI, I am not the only one in this camp because the above library that declared the typings giving the error is by AWS. The naming conventions and functionality of mixed types and union types are just really confusing.

[dragomirtitian]

When first encountering intersection and union types it is easy to be confused about why they are named this way (I know I was). You have to think of types in terms of describing sets of instances.

A union type (|) is the set of instances that belong to either constituent in the union (so for string | number an instances is in the set described by the union if it is either in the set described by number or the set described by string).

The question is having such a type what can we SAFELY do with it? The answer is we can safely access only common members (member which we know to be present regardless of the union constituent an instance actually belongs to). This is where the confusion usually comes in, since the safe members are the intersection of members from the constituent types. But the name union type, refers to the set described by the type not what members we can access.

Same reasoning applies to intersection types (&). The set described by an intersection type is the set of instances that belong simultaneously to both constituents of an intersection (So { a: number } & { b: string } represents a type where an instance is at the same type an instance of { a: number } and an instance of { b: string }). SInce the instance is an instance of both of the constituents types at the same type, we can safely access members of either constituents resulting in a union of members, but again the name is not related to members we can access but to the set operation described by the type.

[RyanCavanaugh]

https://stackoverflow.com/questions/38855908/naming-of-typescripts-union-and-intersection-types

[RyanCavanaugh]

Didn't mean to reopen. Anyway here's a picture

[paseaf]

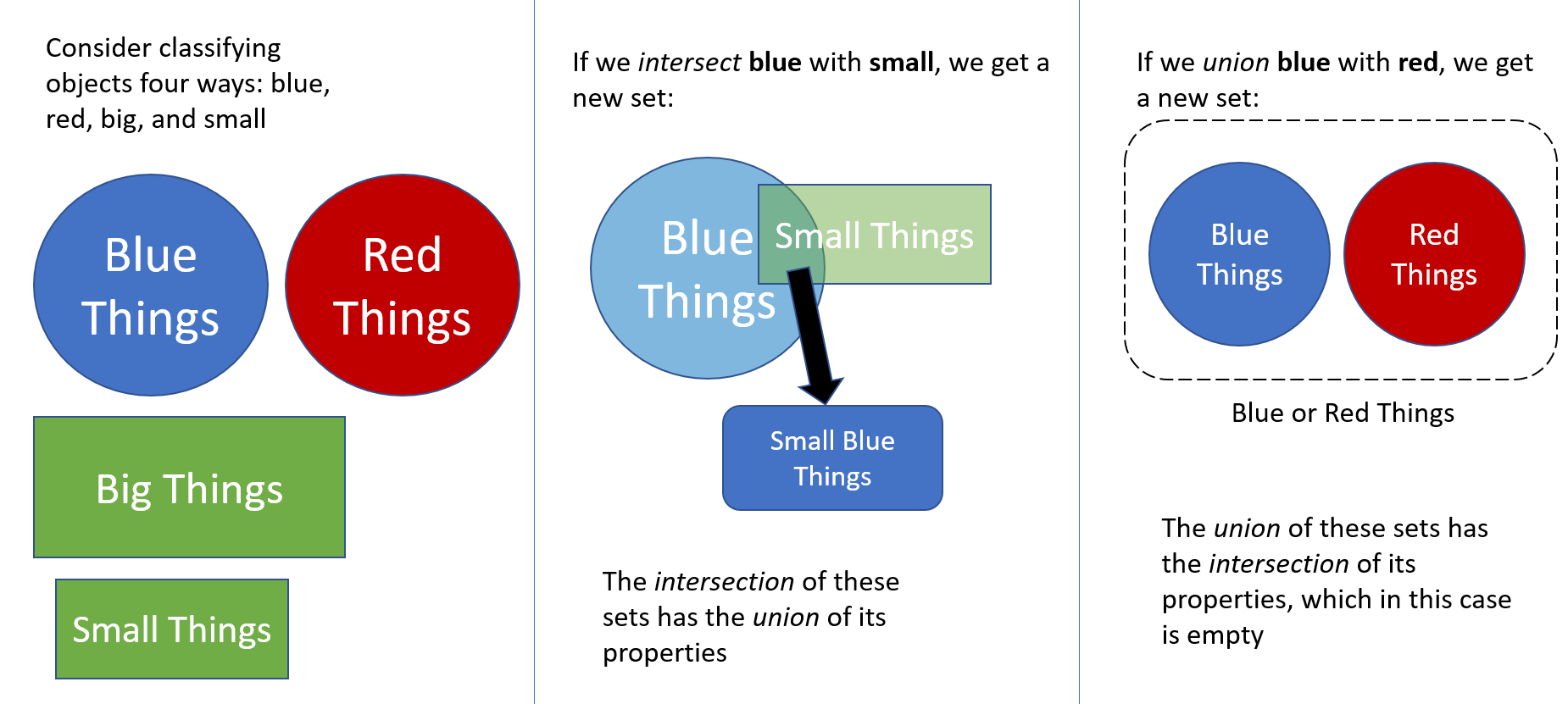
Didn't mean to reopen. Anyway here's a picture

The picture looks confusing because it's not clear what exactly are being operated on and how the operations are defined.
If Pic 2 is true, then it seems like doing set operations, and object properties are being operated on.

If we define four sets in pic 1 in the following way:

Blue_Things = {x in Things | x.color = 'blue'}
Red_Things = {x in Things | x.color = 'red'}
Big_Things = {x in Things | x.size = 'big'}
Small_Things = {x in Things | x.size = 'small'}

Then pic 2 is reasonable if we do set intersection:

intersect(Blue_Things, Small_Things)
= intersect({x in Things | x.color = 'blue'}, {x in Things | x.size = 'small'})
= {x in Things | x.color = 'blue' and x.size = 'small'}
= Small_Blue_Things

But the result of pic 3 is not empty if we do set union:

union(Blue_Things, Red_Things)
= union({x in Things | x.color = 'blue'}, {x in Things | x.color = 'red'})
= {x in Things | x.color = 'blue' or x.color = 'red'}
!= empty

Or maybe the question just cannot be easily explained to people who don't know type theory?

[paseaf]

I think Union and Intersection in TS are confusing because their names look like Set operations, but they are actually not. And the result happen to be the opposite if we understand them as set operations.

• Union | in TS === XOR\
  Union Operator | in TS is actually doing XOR / Either Or on types, but the result is equivalent to doing Set Intersection on type properties

• Intersection & in TS === Combining\
  Intersection Operator & in TS actually doing Combining on types, but the result is equivalent to doing Set Union on type properties

Example:

Let item a value of arbitrary type.\
Let Type_A = {foo: number, bar: int}, Type_B = {bar: int, baz: string}

• the Intersection Type Type_A & Type_B: \
  Defining item of Type_A & Type_B means item is the combination of Type_A and Type_B, which is actually {foo: number, bar: int, baz: string}. Then it is safe to allow item.foo, item.bar, and item.baz.\
  Hence, we have
  Type_A & Type_B = {foo: number, bar: int, baz: string}

• the Union Type Type_A | Type_B:\
  Defining item of Type_A | Type_B means item is either Type_A or Type_B. Then it is unsafe to allow item.foo, because that's an error if the actual item is of Type_B. Similarly, accessing item.baz is also unsafe. \
  Hence, we have
  Type_A | Type_B = {bar: int}

[RyanCavanaugh]

The names are not backwards. Read the StackOverflow link, or a book on type theory.