TypeScripts Type System is Turing Complete
This is not really a bug report and I certainly don't want TypeScripts type system being restricted due to this issue. However, I noticed that the type system in its current form (version 2.2) is turing complete.
Turing completeness is being achieved by combining mapped types, recursive type definitions, accessing member types through index types and the fact that one can create types of arbitrary size.
In particular, the following device enables turing completeness:
type MyFunc<TArg> = {
"true": TrueExpr<MyFunction, TArg>,
"false": FalseExpr<MyFunc, TArg>
}[Test<MyFunc, TArg>];
with TrueExpr, FalseExpr and Test being suitable types.
Even though I didn't formally prove (edit: in the meantime, I did - see below) that the mentioned device makes TypeScript turing complete, it should be obvious by looking at the following code example that tests whether a given type represents a prime number:
type StringBool = "true"|"false";
interface AnyNumber { prev?: any, isZero: StringBool };
interface PositiveNumber { prev: any, isZero: "false" };
type IsZero<TNumber extends AnyNumber> = TNumber["isZero"];
type Next<TNumber extends AnyNumber> = { prev: TNumber, isZero: "false" };
type Prev<TNumber extends PositiveNumber> = TNumber["prev"];
type Add<T1 extends AnyNumber, T2> = { "true": T2, "false": Next<Add<Prev<T1>, T2>> }[IsZero<T1>];
// Computes T1 * T2
type Mult<T1 extends AnyNumber, T2 extends AnyNumber> = MultAcc<T1, T2, _0>;
type MultAcc<T1 extends AnyNumber, T2, TAcc extends AnyNumber> =
{ "true": TAcc, "false": MultAcc<Prev<T1>, T2, Add<TAcc, T2>> }[IsZero<T1>];
// Computes max(T1 - T2, 0).
type Subt<T1 extends AnyNumber, T2 extends AnyNumber> =
{ "true": T1, "false": Subt<Prev<T1>, Prev<T2>> }[IsZero<T2>];
interface SubtResult<TIsOverflow extends StringBool, TResult extends AnyNumber> {
isOverflowing: TIsOverflow;
result: TResult;
}
// Returns a SubtResult that has the result of max(T1 - T2, 0) and indicates whether there was an overflow (T2 > T1).
type SafeSubt<T1 extends AnyNumber, T2 extends AnyNumber> =
{
"true": SubtResult<"false", T1>,
"false": {
"true": SubtResult<"true", T1>,
"false": SafeSubt<Prev<T1>, Prev<T2>>
}[IsZero<T1>]
}[IsZero<T2>];
type _0 = { isZero: "true" };
type _1 = Next<_0>;
type _2 = Next<_1>;
type _3 = Next<_2>;
type _4 = Next<_3>;
type _5 = Next<_4>;
type _6 = Next<_5>;
type _7 = Next<_6>;
type _8 = Next<_7>;
type _9 = Next<_8>;
type Digits = { 0: _0, 1: _1, 2: _2, 3: _3, 4: _4, 5: _5, 6: _6, 7: _7, 8: _8, 9: _9 };
type Digit = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9;
type NumberToType<TNumber extends Digit> = Digits[TNumber]; // I don't know why typescript complains here.
type _10 = Next<_9>;
type _100 = Mult<_10, _10>;
type Dec2<T2 extends Digit, T1 extends Digit>
= Add<Mult<_10, NumberToType<T2>>, NumberToType<T1>>;
function forceEquality<T1, T2 extends T1>() {}
function forceTrue<T extends "true">() { }
//forceTrue<Equals< Dec2<0,3>, Subt<Mult<Dec2<2,0>, _3>, Dec2<5,7>> >>();
//forceTrue<Equals< Dec2<0,2>, Subt<Mult<Dec2<2,0>, _3>, Dec2<5,7>> >>();
type Mod<TNumber extends AnyNumber, TModNumber extends AnyNumber> =
{
"true": _0,
"false": Mod2<TNumber, TModNumber, SafeSubt<TNumber, TModNumber>>
}[IsZero<TNumber>];
type Mod2<TNumber extends AnyNumber, TModNumber extends AnyNumber, TSubtResult extends SubtResult<any, any>> =
{
"true": TNumber,
"false": Mod<TSubtResult["result"], TModNumber>
}[TSubtResult["isOverflowing"]];
type Equals<TNumber1 extends AnyNumber, TNumber2 extends AnyNumber>
= Equals2<TNumber1, TNumber2, SafeSubt<TNumber1, TNumber2>>;
type Equals2<TNumber1 extends AnyNumber, TNumber2 extends AnyNumber, TSubtResult extends SubtResult<any, any>> =
{
"true": "false",
"false": IsZero<TSubtResult["result"]>
}[TSubtResult["isOverflowing"]];
type IsPrime<TNumber extends PositiveNumber> = IsPrimeAcc<TNumber, _2, Prev<Prev<TNumber>>>;
type IsPrimeAcc<TNumber, TCurrentDivisor, TCounter extends AnyNumber> =
{
"false": {
"true": "false",
"false": IsPrimeAcc<TNumber, Next<TCurrentDivisor>, Prev<TCounter>>
}[IsZero<Mod<TNumber, TCurrentDivisor>>],
"true": "true"
}[IsZero<TCounter>];
forceTrue< IsPrime<Dec2<1,0>> >();
forceTrue< IsPrime<Dec2<1,1>> >();
forceTrue< IsPrime<Dec2<1,2>> >();
forceTrue< IsPrime<Dec2<1,3>> >();
forceTrue< IsPrime<Dec2<1,4>>>();
forceTrue< IsPrime<Dec2<1,5>> >();
forceTrue< IsPrime<Dec2<1,6>> >();
forceTrue< IsPrime<Dec2<1,7>> >();
Besides (and a necessary consequence of being turing complete), it is possible to create an endless recursion:
type Foo<T extends "true", B> = { "true": Foo<T, Foo<T, B>> }[T];
let f: Foo<"true", {}> = null!;
Turing completeness could be disabled, if it is checked that a type cannot use itself in its definition (or in a definition of an referenced type) in any way, not just directly as it is tested currently. This would make recursion impossible.
//edit:
A proof of its turing completeness can be found here
All 52 comments
Just a pedantic tip, we might need to implement a minimal language to prove TypeScript is turing complete.
http://stackoverflow.com/questions/449014/what-are-practical-guidelines-for-evaluating-a-languages-turing-completeness
https://sdleffler.github.io/RustTypeSystemTuringComplete/
hmmm, it seems this cannot prove turing completeness.
Nat in this example will always terminate. Because we cannot generate arbitrary natural number. If we do encode some integers, isPrime will always terminate. But Turing machine can loop forever.
That's pretty interesting.
Have you looked into using this recursion so as to say iterate over an array for the purpose of e.g. doing a type-level reduce operation? I'd wanted to look into that before to type a bunch more operations that so far did not seem doable, and your idea here already seems half-way there.
The idea of doing array iteration using type-level recursion is raising a few questions which I'm not sure how to handle at the type level yet, e.g.:
arr.length: obtaining type-level array length to judge when iteration might have finished handling the entire array.- destructuring: how to destructure arrays at the type level so as to separate their first type from the rest. getting the first one is easy (
[0]), destructuring such as to get the rest into a new array, not so sure...
So, TS can prove False? (as in Curry-Howard)
I think stacks a typed length and with each item having an individual type should be possible by adding an additional type parameter and field to the numbers from my example above and storing the item in the number. Two stacks are half the way to proving formal turing completeness, the missing half is to implement a finite automata on top of that.
However, this is a complex and time consuming task and the typical reason why people want to disprove turing completeness in typesystems is that they don't want the compiler to solve the halting problem since that could take forever. This would make life much harder for tooling as you can see in cpp. As I already demonstrated, endless recursions are already possible, so proving actual turing completeness is not that important anymore.
@be5invis What do you mean with that?
@HerringtonDarkholme
I've implemented a turing machine interpreter: https://gist.github.com/hediet/63f4844acf5ac330804801084f87a6d4
@hediet: Yeah, good point that in the absence of a way to infer type-level tuple length, we might get around that by manually supplying it. I suppose that'd also answer the destructuring question, as essentially you'd just keep picking out arr[i] at each iteration, using it to calculate an update reduce() accumulator. It'd no longer be very composable if the length could not be read on the fly, but it's still something -- and perhaps this would be relatively trivial to improve on for TS, anyway.
I suppose that still leaves another question to actually pull off the array iteration though. It's coming down to the traditional for (var i = 0; i < arr.length; i++) {} logic, and we've already side-stepped the .length bit, while the assignment is trivial, and you've demonstrated a way to pull off addition on the type level as well, though not nearly as trivial.
The remaining question for me would be how to deal with the iteration check, whether as i < arr.length or, if reversed, i == 0. It'd be nice if one could just use member access to distinguish the cases, e.g. { 0: ZeroCase, [rest: number]: ElseCase }[i], but this fails as it requires ZeroCase to sub-type ElseCase.
It feels like you've covered exactly these kind of binary checks in your Test<MyFunc, TArg> case. but it seems to imply a type-level function (MyFunc) that could do the checks (returning true / false or your string equivalents). I'm not sure if we have a type-level == (or <) though, do we?
Disclaimer: my understanding of the general mechanisms here may not be as far yet.
So I think where this would get more interesting is if we could do operations on regular type-level values (e.g. type-level 1 + 1, 3 > 0, or true && false). Inspired by @hediet's accomplishment, I tried exploring this a bit more here.
Results:
- Spoiler: I haven't pulled off array iteration.
- I think I've figured out boolean operations (be it using 0/1, like string here) except
Eq. - I think type checks (type-level
InstanceOf,Matches,TypesEq) could be done if #6606 lands (alternatives?). - I'm not sure how to go about number/array operators without more to go by. Array (= vector/tuple) iteration seems doable given a way to increment numbers -- or a structure like @hediet used, if it could be construed from the array. Conversely, number operations could maybe be construed given operations on bit vectors and a way to convert those back and forth... tl;dr kinda stumped.
These puzzles probably won't find solutions anytime soon, but if anything, this does seem like one thread where others might have better insights...
I made some progress, having tried to adapt the arithmetic operators laid out in the OP so as to work with number literals instead of special types. Skipped prime number stuff, but did add those operators like > etc.
The downside is I'm storing a hard-coded list of +1 increments, making it scale less well to higher numbers. Or negatives. Or fractions.
I mainly wanted to use them for that array iteration/manipulation though. Iteration works, and array manipulation, well, we can 'concatenate' tuple types by constructing a numeric object representing the result (with length to satisfy the ArrayLike interface if desired).
I'm honestly amazed we got this far with so few operators. I dunno much about Turing completeness, but I guess functions seem like the next frontier now.
@be5invis You're thinking of an unsound type system. Turing completeness merely makes type checking undecidable. So, you can't prove false, but you can write something that is impossible to prove or disprove.
@aij TypeScript has its fair share of unsoundness too: https://github.com/Microsoft/TypeScript/issues/8459
This is like c++ template metaprogramming ?
@iamandrewluca From what I understand -- yes.
Turing completeness could be disabled, if it is checked that a type cannot use itself in its definition (or in a definition of an referenced type) in any way, not just directly as it is tested currently. This would make recursion impossible.
Possible relevant tickets:
- https://github.com/Microsoft/TypeScript/issues/6230
- https://github.com/Microsoft/TypeScript/issues/3496#issuecomment-128553540
I'm just wondering if this would affect how recursive type definitions are currently handled by TypeScript.
If TypeScript uses eager type checking for direct type usages but not interface type usages, then would this restriction still preserve the interface trick for recursive type definitions?
so we can we write an undecidable type in ts, cant we?
so we can we write an undecidable type in ts, cant we?
Assuming TypeScript type system is indeed Turning complete, yes.
For any TS compiler, there would be a program that the compiler could not correctly type check.
Whether this matters practically is an entirely different story. There are already programs you could not compile, due to limited stack space, memory, etc. on your computer.
@pauldraper:
Whether this matters practically is an entirely different story. There are already programs you could not compile, due to limited stack space, memory, etc. on your computer.
If you try to take idiomatic functional programming concepts from JS to TS (generics, currying, composition, point-free function application), type inference breaks down pretty much immediately. The run-time JS though runs fine. Hardware isn't the bottleneck there.
@pauldraper
For any TS compiler, there would be a program that the compiler could not correctly type check.
This is true regardless of whether the type system itself is Turing-complete.
function dec(n: number): boolean {
return n === 0 ? true : dec(n - 1);
}
let x: boolean = dec(10) ? true : 42;
TypeScript can't typecheck this program, even though it doesn't evaluate to an error.
Turing Completeness in the type-system just means type-checking now returns yes/no/loop, but this can be dealt with by bounding the type-checker (which I think already happens).
@tycho01 checking !== inferring (Though I agree with your point).
TypeScript can't typecheck this program, even though it doesn't evaluate to an error.
What do you mean? The TS compiler checks that program just fine and properly finds the type-error?
@paldepind The point is that the else clause of the ternary is unreachable so the program should in fact pass the type checker (but it does not); i.e., dec(10) returns true (and 10 is a compile time constant/literal).
@johanatan Just because the else clause is never taken doesn't make the program well-typed. Generally how code is actually run during execution does not affect whether or not a program is well-typed. If you look at the specification it states that the type of a conditional expression is the union of the types of the two expressions (i.e. the if and the else case). Thus, dec(10) ? true : 42; has the type boolean | number and hence you example is ill-typed. That error is correctly reported by the TS compiler.
@paldepind
The meaning of being well-typed is fundamentally linked to run-time behavior. Milner [1] coined the phrase _well-typed programs cannot 'go wrong'_, where going 'wrong' has a specific definition.
A type system is _sound_ if any well-typed program cannot go wrong. A type system is _complete_ if any program that cannot go wrong is well-typed.
The example program does not go wrong and therefore TypeScript is giving a false-positive by reporting a type error.
[1] A theory of type polymorphism in programming (1978)
@jack-williams
That is a good quote. But, I think there's a difference between saying "well-typed programs cannot 'go wrong'" and saying "programs that don't 'go wrong' are well-typed". The implication is in different directions. The first statement is valid (Milner said it) but I don't think the second is.
The example program doesn't go wrong. But that does not make it well-typed. A program is well-typed if it satisfies the typing rules of the given language. The example program does not satisfy the typing rules of TypeScript and thus it is not well-typed.
@johanatan wrote that "the program should, in fact, pass the type checker" because the program doesn't go wrong. But, that is not the criteria that decide if a program should pass a type-checker. A program should pass a type-checker if it satisfies the typing rules of a language. And the program in question does not.
Soundness and completeness are properties of the _type system_. Whether or not a program is well-typed is a property of the _program_ in relation to the type system. These things are unrelated. As an example simply typed lambda calculus it both sound and complete. But, still it is easy to write a program in lambda calculus that doesn't 'go wrong' at run-time but which would still not be well-typed according to the simply typed lambda calculus type-system. That is an example of "doesn't go wrong does not imply well-typed".
Anyway, it is possible that I may have gotten something wrong. In that case, please correct me 😄
Including perfect reachability analysis in a definition of completeness is very questionable because it implies that any truly complete type system could be used to e.g. prove or disprove the Collatz conjecture:
BigInt n = 0;
while(CollatzTerminates(n)) n++;
// Collatz is true iff this program is well-typed
"foo" * 3;
But, I think there's a difference between saying "well-typed programs cannot 'go wrong'" and saying "programs that don't 'go wrong' are well-typed". The implication is in different directions.
Yes this is exactly right; though I wasn't suggesting that they were the same.
A program is well-typed if it satisfies the typing rules of the given language. The example program does not satisfy the typing rules of TypeScript and thus it is not well-typed.
I'm not saying that the definition of being well-typed is not going wrong. You're free to define it as you say. However that definition alone tells us very little; we can _say_ that something satisfies the rules but what does that _mean_? How would we compare one checker for JavaScript with another? I could come up with a set of ad-hoc rules that let you write buggy programs that are technically well-typed, but my notion of being well-typed is inferior to TypeScript's.
So it's helpful to have an external notion, which has long been the class of 'safe' programs that don't get stuck during evaluation. With that I can talk to someone about my system and tell them what it means to be well-typed in my system, without depending on the specific rules of my system.
While we expect most systems to be sound with respect to this notion of 'safe programs', programmers have happily lived with the fact that we can't have completeness. Programmers wont be able to write programs they know to be safe because the type-checker will get in the way.
Adding Turing Completeness to the type system isn't such a big deal because the undecidability can be exchanged for incompleteness by bounding the checker, and programmers have already been living with incompleteness. That was my only real point!
@RyanCavanaugh Yes completeness gets thrown away once the source language is turing-complete, because for the type-system to be complete it would need to be able to solve the halting problem.
I completely agree with what @jack-williams stated above and, yes, according to the rules of the TypeScript type system, what I stated was incorrect.
However, the line between "compile-time" and "run-time" is quite blurred these days via several techniques: multi-stage programming & refinement types to name a couple. In the former, one can think of runtime as merely the final "stage" (and clearly from a human perspective we can reason at any number of meta- levels).
@RyanCavanaugh Gödel's incompleteness theorems still apply here, via the Curry–Howard isomorphism.
{Complete, Sound, Decidable}: Pick two. (or fewer)
@jack-williams @johanatan I fully agree with both of your latest comments. So it seems that we agree :smile:
@aij
{Complete, Sound, Decidable}: Pick two. (or fewer)
That is not the entire story though. You can have completeness, soundness, and decidability at the same time. Simply typed lambda calculus is a case in point. Then you have to forego Turing completeness. Sometimes that is the appropriate tradeoff. For instance in languages like Coq and Idris.
You probably know that but I just wanted to point it out.
https://github.com/zuozijian3720/24game
author @zuozijian3720
Came up a way to concatenate tuples in typescript@next, it's not practical, but I think it helps for people investing fun. Expecting typescript type system being better.
type ToTuple<T> = T extends any[] ? T : any[];
type Head<Tuple extends any[]> = Tuple extends [infer H, ...any[]] ? H : never;
type Tail<Tuple extends any[]> = ((...t: Tuple) => void) extends ((h: any, ...rest: infer R) => void) ? R : never;
type Unshift<Tuple extends any[], Element> = ((h: Element, ...t: Tuple) => void) extends (...t: infer R) => void ? R : never;
type Push<Tuple extends any[], Element, R = Reverse<Tuple>, T extends any[]= ToTuple<R>> = Reverse<Unshift<T, Element>>;
type Reverse<Tuple extends any[]> = Reverse_<Tuple, []>;
type Reverse_<Tuple extends any[], Result extends any[]> = {
1: Result,
0: Reverse_<Tail<Tuple>, Unshift<Result, Head<Tuple>>>
}[Tuple extends [] ? 1 : 0];
type Concat<Tuple1 extends any[], Tuple2 extends any[], R = Reverse<Tuple1>, T extends any[]= ToTuple<R>> = Concat_<T, Tuple2>;
type Concat_<Tuple1 extends any[], Tuple2 extends any[]> = {
1: Reverse<Tuple1>,
0: Concat_<Unshift<Tuple1, Head<Tuple2>>, Tail<Tuple2>>,
}[Tuple2 extends [] ? 1 : 0];
type x = Concat<[1, 2, 3], [4, 5, 6]>; // [1, 2, 3, 4, 5, 6]
You can do math relatively efficiently if you instead use a LUT and do it digit-by-digit:
https://github.com/aman-tiwari/shape-types/blob/master/index.ts
@jack-williams
For any TS compiler, there would be a program that the compiler could not correctly type check.
This is true regardless of whether the type system itself is Turing-complete.
"Correct type check" means verify types according to the language specification.1 If you take "correct type check" to be "verify there are no runtime errors" ... then yes, no compiler of TS, Java, Lisp, COBOL or any other Turning-complete language can provide those assurances.
It's such a meaningless interpretation as to be irrelevant. Type checking is performed according to the language specification, period. And in the case of TS, the language specification describes a Turing-complete type language (in addition to the obviously Turning-complete language itself).
1 https://github.com/Microsoft/TypeScript/blob/master/doc/spec.md Though it's really out of date right now; I think the current spec exists only in the minds of TS authors (and maybe not even then).
I wanted to see how far can I push it and built a Bracket Expression verifier using @fightingcat 's Tuples and @hediet 's awesome example and automata.
https://github.com/Crypto-Punkers/labs/blob/master/metaprogramming/src/brackets.ts
One interesting thing I've noticed is that it's easy to lose typing information with Tuples, as the TSC will happy convert them into more general forms when for example passing it inside generics.
type Tail<Tuple extends any[]> = ((...t: Tuple) => void) extends ((
h: any,
...rest: infer R
) => void)
? R
: never;
type IsEmpty<Tuple extends any[]> = {
true: "true";
false: "false";
}[Tuple extends [] ? "true" : "false"];
type Next<Tuple extends any[], TState extends State<any>> = {
value: Tail<TState["value"]>;
};
type SpecificTuple = [1, 2, 3];
type State<Tuple extends any[]> = { value: Tuple };
type Result = Next<SpecificTuple, State<SpecificTuple>>;
//Actual result:
// type Result = {
// value: any[];
// };
//Favourable result:
// type Result = {
// value: [2, 3];
// };
type Next<Tuple extends any[], TState extends State<any>> = {
value: Tail<TState extends State<infer R> ? R : never>;
};
@ritave You can change your Next to like this.
A way to convert union to tuple, we have ability to iterate properties now.
@fightingcat nice, does this make a custom implemented Merge type possible?
@hediet No need for this, there is already a trick doing the union-to-intersection
Type-level addition, using tuples for natural numbers and 0|1|2|3|4|5|6|7|8|9 for digits.
type PopFront<TupleT extends any[]> = (
((...tuple : TupleT) => void) extends ((head : any, ...tail : infer TailT) => void) ?
TailT :
never
);
type PushFront<TailT extends any[], FrontT> = (
((front : FrontT, ...tail : TailT) => void) extends ((...tuple : infer TupleT) => void) ?
TupleT :
never
);
type ReverseImpl<InputT extends any[], OutputT extends any[]> = {
0 : OutputT,
1 : ReverseImpl<PopFront<InputT>, PushFront<OutputT, InputT[0]>>
}[
InputT["length"] extends 0 ?
0 :
1
];
type Reverse<InputT extends any[]> = (
ReverseImpl<InputT, []> extends infer X ?
(
X extends any[] ?
X :
never
) :
never
);
type LeftPadImpl<TupleT extends any[], ElementT extends any, LengthT extends number> = {
0 : TupleT,
1 : LeftPad<PushFront<TupleT, ElementT>, ElementT, LengthT>
}[
TupleT["length"] extends LengthT ?
0 :
1
];
type LeftPad<TupleT extends any[], ElementT extends any, LengthT extends number> = (
LeftPadImpl<TupleT, ElementT, LengthT> extends infer X ?
(
X extends any[] ?
X :
never
) :
never
);
type LongerTuple<A extends any[], B extends any[]> = (
keyof A extends keyof B ?
B :
A
);
///////////////////////////////////////////////////////
type Digit = 0|1|2|3|4|5|6|7|8|9;
/**
* A non-empty tuple of digits
*/
type NaturalNumber = Digit[];
/**
* 6 - 1 = 5
*/
type SubOne<D extends Digit> = {
0 : never,
1 : 0,
2 : 1,
3 : 2,
4 : 3,
5 : 4,
6 : 5,
7 : 6,
8 : 7,
9 : 8,
}[D];
/**
*
* 9 + 1 = 10
*
* The ones place of `10` is `0`
*/
type AddOne_OnesPlace<D extends Digit> = {
0 : 1,
1 : 2,
2 : 3,
3 : 4,
4 : 5,
5 : 6,
6 : 7,
7 : 8,
8 : 9,
9 : 0
}[D];
/**
*
* 7 + 8 = 15
*
* The ones place of `15` is `5`
*/
type AddDigit_OnesPlace<A extends Digit, B extends Digit> = {
0 : B,
1 : AddDigit_OnesPlace<SubOne<A>, AddOne_OnesPlace<B>>
}[
A extends 0 ?
0 :
1
];
//4
type addDigit_OnesPlace_0 = AddDigit_OnesPlace<6, 8>;
//6
type addDigit_OnesPlace_1 = AddDigit_OnesPlace<8, 8>;
//0
type addDigit_OnesPlace_2 = AddDigit_OnesPlace<9, 1>;
/**
* 7 + 8 = 15
*
* Since it is `15 >= 10`, we have a carry
*/
type AddDigit_Carry<A extends Digit, B extends Digit> = {
0 : false,
1 : (
AddOne_OnesPlace<B> extends 0 ?
true :
AddDigit_Carry<SubOne<A>, AddOne_OnesPlace<B>>
)
}[
A extends 0 ?
0 :
1
];
/*
type AddDigit_Carry<A extends Digit, B extends Digit> = (
LtDigit<
AddDigit_OnesPlace<A, B>,
A
>
);
*/
//true
type addDigit_carry_0 = AddDigit_Carry<7, 8>;
//true
type addDigit_carry_1 = AddDigit_Carry<9, 1>;
//false
type addDigit_carry_2 = AddDigit_Carry<8, 1>;
type AddDigitWithCarry_OnesPlace<A extends Digit, B extends Digit, CarryT extends boolean> = (
CarryT extends true ?
(
B extends 9 ?
(
A extends 9 ?
(
//9+9+1 = 19
9
) :
(AddDigit_OnesPlace<AddOne_OnesPlace<A>, B>)
) :
(AddDigit_OnesPlace<A, AddOne_OnesPlace<B>>)
) :
AddDigit_OnesPlace<A, B>
);
type AddDigitWithCarry_Carry<A extends Digit, B extends Digit, CarryT extends boolean> = (
CarryT extends true ?
(
B extends 9 ?
(
A extends 9 ?
(
//9+9+1 = 19
true
) :
(AddDigit_Carry<AddOne_OnesPlace<A>, B>)
) :
(AddDigit_Carry<A, AddOne_OnesPlace<B>>)
) :
AddDigit_Carry<A, B>
);
/**
* + Assumes `A` and `B` have the same length.
* + Assumes `A` and `B` have been reversed.
* So, `A[0]` is actually the **LAST** digit of the number.
*/
type AddNaturalNumberImpl<
A extends NaturalNumber,
B extends NaturalNumber,
ResultT extends NaturalNumber,
CarryT extends boolean
> = {
0 : (
AddDigitWithCarry_Carry<A[0], B[0], CarryT> extends true ?
PushFront<
PushFront<
ResultT,
AddDigitWithCarry_OnesPlace<
A[0],
B[0],
CarryT
>
>,
1
> :
PushFront<
ResultT,
AddDigitWithCarry_OnesPlace<
A[0],
B[0],
CarryT
>
>
),
1 : (
AddNaturalNumberImpl<
PopFront<A>,
PopFront<B>,
PushFront<
ResultT,
AddDigitWithCarry_OnesPlace<
A[0],
B[0],
CarryT
>
>,
AddDigitWithCarry_Carry<A[0], B[0], CarryT>
>
)
}[
A["length"] extends 1 ?
0 :
1
];
type AddNaturalNumber<
A extends NaturalNumber,
B extends NaturalNumber
> = (
AddNaturalNumberImpl<
Reverse<LeftPad<A, 0, LongerTuple<A, B>["length"]>>,
Reverse<LeftPad<B, 0, LongerTuple<A, B>["length"]>>,
[],
false
>
);
//101264
export type addNaturalNumber_0 = AddNaturalNumber<
[5,2,3,4,1],
[4,8,9,2,3]
>;
//49446
export type addNaturalNumber_1 = AddNaturalNumber<
[5,2,3],
[4,8,9,2,3]
>;
//49446
export type addNaturalNumber_2 = AddNaturalNumber<
[4,8,9,2,3],
[5,2,3]
>;
//980
export type addNaturalNumber_3 = AddNaturalNumber<
[5,7],
[9,2,3]
>;
@jcalz (circular conditional type police)
//36893488147419103230
export type addNaturalNumber_bigint = AddNaturalNumber<
//Max bigint value for MySQL: https://docs.oracle.com/cd/E17952_01/mysql-5.0-en/integer-types.html
[1,8,4,4,6,7,4,4,0,7,3,7,0,9,5,5,1,6,1,5],
[1,8,4,4,6,7,4,4,0,7,3,7,0,9,5,5,1,6,1,5]
>;
Just leaving this here by @acutmore
https://gist.github.com/acutmore/9d2ce837f019608f26ff54e0b1c23d6e
thanks @AnyhowStep - this issue thread was what originally inspired that gist :)
One challenge I kept hitting was _'Type instantiation is excessively deep and possibly infinite'_. Thankfully turns out can use a good old fashioned trampoline to increase the limit. I had to put one trampoline inside another to get the limit high enough. Might be useful to someone else:
type Prepend<V extends any, Arr extends any[]> =
((v: V,...a: Arr) => any) extends (...a: infer Args) => any
? Args
: [];
// Normal NTuple
type NTuple<N extends number, __accumulator extends any[] = []> = {
0: NTuple<N, Prepend<any, __accumulator>>
1: __accumulator
}[__accumulator["length"] extends N ? 1 : 0];
type Tuple5 = NTuple<5>; // [any, any, any, any, any]
type Tuple49 = NTuple<43>; // Err! Type instantiation is excessively deep and possibly infinite.
// NTuple again with a trampoline
type NTupleTrampoline<
N extends number,
__bounce extends any = Trampoline<N, [], []>
> = {
0: NTupleTrampoline<N, Trampoline<N, __bounce['state'], []>>
1: __bounce['state']
}[__bounce["tag"] extends 'done' ? 1 : 0];
type Trampoline<
N extends number,
Accumulator extends any[],
NumberOfBounces extends any[]
> = {
0: Trampoline<N, Prepend<any, Accumulator>, Prepend<any, Accumulator>>;
1: { tag: 'done', state: Accumulator }
2: { tag: 'bounce', state: Accumulator }
}[Accumulator["length"] extends N
? 1
: NumberOfBounces["length"] extends 30
? 2
: 0];
type Tuple5Bounced = NTupleTrampoline<60>; // No Error, [any * 60]
@acutmore check this out
up to 288 elements with simpiler logic.
type NTuple<T, N extends number> = __increase<T, N, []>;
// increase by 8 if U has smaller size, otherwise goto decreasing
type __increase<T, N extends number, U extends T[]> = {
0: __increase<T, N, Unshift8<U, T>>;
1: __decrease<T, N, U>;
}[N extends Partial<U>['length'] ? 1 : 0];
// decrease by 1 if U has larger size, otherwise return U
type __decrease<T, N extends number, U extends T[]> = {
0: __decrease<T, N, Drop<U>>;
1: U;
}[U['length'] extends N ? 1 : 0];
type Unshift8<U extends T[], T> = ((a: T, b: T, c: T, d: T, e: T, f: T, g: T, h: T, ...t: U) => void) extends (...t: infer R) => void ? R : never;
type Drop<T extends any[]> = ((...t: T) => void) extends (x: any, ...t: infer R) => void ? R : never;
type tuple288 = NTuple<number, 288>;
update: up to 496 elements
Just add Unshift32 and get more
slightly refactored the code :)
We need a typescript backend that targets this 4 bit VM :D
How does your interpreted time correlate with interpretion time, @acutmore? For my turing machine implementation it sadly wasn't linear.
Good news everyone, I'm working on an interpreted language with typescript type system, parser implemented, I'll update once everything is complete.
The grammar looks like this:
type ast = ParseSource<[
If, 1, add, 2, eq, 3, [
Print, "1 + 2 = 3"
],
Else, [
Print, "The world is crazy."
]
]>;
I got a hunch maybe I can even implement function and type XD
update: refactored the parser, now code is much much more readable, now working on the evaluator, implemented convertion between number and binary by hard-coding a binary tree.....
Demonstration of number convertion
@fightingcat my goodness. I thought the round-trip might have been a bamboozle, but nope...
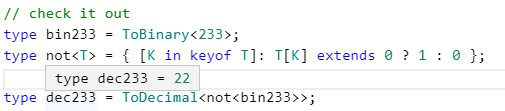
@RyanCavanaugh I'm almost done, have implemented parser and arithmetics, right now there is a working expression evaluator, I've pushed to the repo.

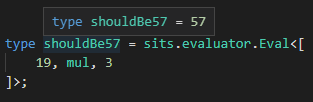

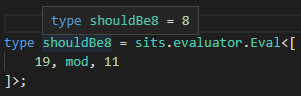
I'm taking a few days off, then I'll finish statements evaluator, and module declarations. I'm afraid loop statement and variable assignment may cause TS2589 easily, but better than not implementing it.
wow @fightingcat! The whole 'sits' repo is a gem to read.
Still trying to grok how your division works, looks much more robust that than my naive "keep subtracting in a recursive type loop" implementation.
@fightingcat This is very impressive work. Keep going!
It might be interesting to implement Presburger arithmetic in TS. Unlike multiplication and division, (i.e. Peano arithmetic), addition, subtraction and comparison are all decidable operations.
My contribution: the problem "That's a Lot of Fish", a TypeScript reverse-engineering challenge, from PlaidCTF 2020. When unmangled, it turns out to be a VM that runs completely in the type system. I might have needed to relax some checks in tsc.js to make it work, though... 😅
The VM supports (arbitrary-precision) addition and multiplication, several bitwise operations, comparison, branching, and function calls. It also has a section of memory that's made up entirely of leftist heaps and supports pushing and polling them as primitive operations.
For the problem, I wrote a little program that checks if the user's input is a minimum-weight Manhattan TSP solution for a graph that's hardcoded in memory, which only typechecks (and outputs out the flag) if the input is correct. When given the correct input, it takes about three and a half minutes to typecheck, which is much faster than I was expecting. (Though I did have to give it 16GB of heap and 8GB of stack to make it not crash.)
I could have sworn there was a repo full of awesome TS work like this, could anyone help me find it again? I know it had things like a solution to a Tower of Hanoi problem, prime number detection, subtraction, addition, etc
I wrote a text adventure in the typescript type system:
- Blog Post: https://ricklove.me/typescript-type-system-adventure
- Repo: https://github.com/ricklove/rick-love-master/tree/master/code/typescript-type-system-adventure

Most helpful comment
@RyanCavanaugh I'm almost done, have implemented parser and arithmetics, right now there is a working expression evaluator, I've pushed to the repo.



