Scikit-learn: Numerical precision of euclidean_distances with float32
Description
I noticed that sklearn.metrics.pairwise.pairwise_distances function agrees with np.linalg.norm when using np.float64 arrays, but disagrees when using np.float32 arrays. See the code snippet below.
Steps/Code to Reproduce
import numpy as np
import scipy
import sklearn.metrics.pairwise
# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875, -65.7512664794921875], dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)
# create 32-bit versions of a and b
a_32 = a_64.astype(np.float32)
b_32 = b_64.astype(np.float32)
# compute the distance from a to b using numpy, for both 64-bit and 32-bit
dist_64_np = np.array([np.linalg.norm(a_64 - b_64)], dtype=np.float64)
dist_32_np = np.array([np.linalg.norm(a_32 - b_32)], dtype=np.float32)
# compute the distance from a to b using sklearn, for both 64-bit and 32-bit
dist_64_sklearn = sklearn.metrics.pairwise.pairwise_distances([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.pairwise_distances([a_32], [b_32])
# note that the 64-bit sklearn results agree exactly with numpy, but the 32-bit results disagree
np.set_printoptions(precision=200)
print(dist_64_np)
print(dist_32_np)
print(dist_64_sklearn)
print(dist_32_sklearn)
Expected Results
I expect that the results from sklearn.metrics.pairwise.pairwise_distances would agree with np.linalg.norm for both 64-bit and 32-bit. In other words, I expect the following output:
[ 0.0229059506440019884643266578905240749008953571319580078125]
[ 0.02290595136582851409912109375]
[[ 0.0229059506440019884643266578905240749008953571319580078125]]
[[ 0.02290595136582851409912109375]]
Actual Results
The code snippet above produces the following output for me:
[ 0.0229059506440019884643266578905240749008953571319580078125]
[ 0.02290595136582851409912109375]
[[ 0.0229059506440019884643266578905240749008953571319580078125]]
[[ 0.03125]]
Versions
Darwin-16.6.0-x86_64-i386-64bit
('Python', '2.7.11 | 64-bit | (default, Jun 11 2016, 03:41:56) \n[GCC 4.2.1 Compatible Apple LLVM 6.0 (clang-600.0.57)]')
('NumPy', '1.11.3')
('SciPy', '0.19.0')
('Scikit-Learn', '0.18.1')
All 102 comments
Same results with python 3.5 :
Darwin-15.6.0-x86_64-i386-64bit
Python 3.5.1 (v3.5.1:37a07cee5969, Dec 5 2015, 21:12:44)
[GCC 4.2.1 (Apple Inc. build 5666) (dot 3)]
NumPy 1.11.0
SciPy 0.18.1
Scikit-Learn 0.17.1
It happens only with euclidean distance and can be reproduced using directly sklearn.metrics.pairwise.euclidean_distances :
import scipy
import sklearn.metrics.pairwise
# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875, -65.7512664794921875], dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)
# create 32-bit versions of a and b
a_32 = a_64.astype(np.float32)
b_32 = b_64.astype(np.float32)
# compute the distance from a to b using sklearn, for both 64-bit and 32-bit
dist_64_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_32], [b_32])
np.set_printoptions(precision=200)
print(dist_64_sklearn)
print(dist_32_sklearn)
I couldn't track down further the error.
I hope this can help.
numpy might use a higher precision accumulator. yes, it looks like this
deserves fixing.
On 19 Jul 2017 12:05 am, "nvauquie" notifications@github.com wrote:
Same results with python 3.5 :
Darwin-15.6.0-x86_64-i386-64bit
Python 3.5.1 (v3.5.1:37a07cee5969, Dec 5 2015, 21:12:44)
[GCC 4.2.1 (Apple Inc. build 5666) (dot 3)]
NumPy 1.11.0
SciPy 0.18.1
Scikit-Learn 0.17.1It happens only with euclidean distance and can be reproduced using
directly sklearn.metrics.pairwise.euclidean_distances :import scipy
import sklearn.metrics.pairwisecreate 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875, -65.7512664794921875], dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)create 32-bit versions of a and b
a_32 = a_64.astype(np.float32)
b_32 = b_64.astype(np.float32)compute the distance from a to b using sklearn, for both 64-bit and 32-bit
dist_64_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_64], [b_64])
dist_32_sklearn = sklearn.metrics.pairwise.euclidean_distances([a_32], [b_32])np.set_printoptions(precision=200)
print(dist_64_sklearn)
print(dist_32_sklearn)I couldn't track down further the error.
I hope this can help.—
You are receiving this because you are subscribed to this thread.
Reply to this email directly, view it on GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-316074315,
or mute the thread
https://github.com/notifications/unsubscribe-auth/AAEz65yy8Aq2FcsDAcWHT8qkkdXF_MfPks5sPLu_gaJpZM4OXbpZ
.
I'd like to work on this if possible
Go for it!
So I think the problem lies around the fact that we are using sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y)) for computing euclidean distance
Because if I try - (-2 * np.dot(X, Y.T) + (X * X).sum(axis=1) + (Y * Y).sum(axis=1) I get the answer 0 for np.float32, while I get the correct ans for np.float 64.
@jnothman What do you think I should do then ? As mentioned in my comment above the problem is probably computing euclidean distance using sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))
So you're saying that dot is returning a less precise result than product-then-sum?
No, what I'm trying to say is dot is returning more precise result than product-then-sum
-2 * np.dot(X, Y.T) + (X * X).sum(axis=1) + (Y * Y).sum(axis=1) gives output [[0.]]
while np.sqrt(((X-Y) * (X-Y)).sum(axis=1)) gives output [ 0.02290595]
It is not clear what you are doing, partly because you are not posting a fully stand-alone snippet.
Quickly looking at your last post the two things you are trying to compare [[0.]] and [0.022...] do not have the same dimensions (maybe a copy and paste problem but again hard to know because we don't have a full snippet).
Ok sorry my bad
import numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot
# create 64-bit vectors a and b that are very similar to each other
a_64 = np.array([61.221637725830078125, 71.60662841796875, -65.7512664794921875], dtype=np.float64)
b_64 = np.array([61.221637725830078125, 71.60894012451171875, -65.72847747802734375], dtype=np.float64)
# create 32-bit versions of a and b
X = a_64.astype(np.float32)
Y = b_64.astype(np.float32)
X, Y = check_pairwise_arrays(X, Y)
XX = row_norms(X, squared=True)[:, np.newaxis]
YY = row_norms(Y, squared=True)[np.newaxis, :]
#Euclidean distance computed using product-then-sum
distances = safe_sparse_dot(X, Y.T, dense_output=True)
distances *= -2
distances += XX
distances += YY
print(np.sqrt(distances))
#Euclidean distance computed using (X-Y)^2
print(np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis]))
OUTPUT
[[ 0.03125]]
[[ 0.02290595136582851409912109375]]
The first method is how it is computed by the euclidean distance function.
Also to clarify what I meant above was the fact that sum-then-product has lower precision even when we use numpy functions to do it
Yes, I can replicate this. I see that doing the subtraction initially
allows the precision of the difference to be maintained. Doing the dot
product and then subtracting (or negating and adding), as we currently do,
loses this precision as the most significant figures are much larger than
the differences.
The current implementation is more memory efficient for a high number of
features. But I suppose euclidean distance becomes increasingly irrelevant
in high dimensions, so the memory is dominated by the number of output
values.
So I vote for adopting the more numerically stable implementation over the
d-asymptotically efficient implementation we currently have. An opinion,
@ogrisel? @agramfort?
And this is of course more of a concern since we recently allowed float32s
to be more commonplace across estimators.
So for this example product-then-sum works perfectly fine for np.float64, so a possible solution could be to convert the input to float64 then compute the result and return the result converted back to float32. I guess this would be more efficient, but not sure if this would work fine for some other example.
converting to float64 won't be more efficient in memory usage than
subtraction.
Oh yeah you are right sorry about that, but I think using float64 and then doing product-then-sum would be more efficient computationally if not memory wise.
And the reason for using product-then-sum was to have more computational efficiency and not memory efficiency.
sure, but I don't believe there is any reason to assume that it is in fact
more computationally efficient except by way of not having to realise an
intermediate array. Assuming we limit absolute working memory (e.g. by
chunking), why would taking the dot product, doubling and subtracting norms
be much more efficient than subtracting and squaring?
Provide benchmarks?
Ok so I created a python script to compare the time taken by subtraction-then-squaring and conversion to float64 then product-then-sum and it turns out if we choose an X and Y as very big vectors then the 2 results are very different. Also @jnothman you were right subtraction-then-squaring is faster.
Here's the script that I wrote, if there's any problem please let me know
import numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot
from timeit import default_timer as timer
for i in range(9):
X = np.random.rand(1,3 * (10**i)).astype(np.float32)
Y = np.random.rand(1,3 * (10**i)).astype(np.float32)
X, Y = check_pairwise_arrays(X, Y)
XX = row_norms(X, squared=True)[:, np.newaxis]
YY = row_norms(Y, squared=True)[np.newaxis, :]
#Euclidean distance computed using product-then-sum
distances = safe_sparse_dot(X, Y.T, dense_output=True)
distances *= -2
distances += XX
distances += YY
ans1 = np.sqrt(distances)
start = timer()
ans2 = np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis])
end = timer()
if ans1 != ans2:
print(end-start)
start = timer()
X = X.astype(np.float64)
Y = Y.astype(np.float64)
X, Y = check_pairwise_arrays(X, Y)
XX = row_norms(X, squared=True)[:, np.newaxis]
YY = row_norms(Y, squared=True)[np.newaxis, :]
distances = safe_sparse_dot(X, Y.T, dense_output=True)
distances *= -2
distances += XX
distances += YY
distances = np.sqrt(distances)
end = timer()
print(end-start)
print('')
if abs(ans2 - distances) > 1e-3:
# np.set_printoptions(precision=200)
print(ans2)
print(np.sqrt(distances))
print(X, Y)
break
it's worth testing how it scales with the number of samples, not just the
number of features... taking norms may have the benefit of computing some
things once per sample, not once per pair of samples
On 20 Oct 2017 2:39 am, "Osaid Rehman Nasir" notifications@github.com
wrote:
Ok so I created a python script to compare the time taken by
subtraction-then-squaring and conversion to float64 then product-then-sum
and it turns out if we choose an X and Y as very big vectors then the 2
results are very different. Also @jnothman https://github.com/jnothman
you were right subtraction-then-squaring is faster.
Here's the script that I wrote, if there's any problem please let me knowimport numpy as np
import scipy
from sklearn.metrics.pairwise import check_pairwise_arrays, row_norms
from sklearn.utils.extmath import safe_sparse_dot
from timeit import default_timer as timerfor i in range(9):
X = np.random.rand(1,3 * (10i)).astype(np.float32)
Y = np.random.rand(1,3 * (10i)).astype(np.float32)X, Y = check_pairwise_arrays(X, Y)
XX = row_norms(X, squared=True)[:, np.newaxis]
YY = row_norms(Y, squared=True)[np.newaxis, :]#Euclidean distance computed using product-then-sum
distances = safe_sparse_dot(X, Y.T, dense_output=True)
distances *= -2
distances += XX
distances += YYans1 = np.sqrt(distances)
start = timer()
ans2 = np.sqrt(row_norms(X-Y, squared=True)[:, np.newaxis])
end = timer()
if ans1 != ans2:
print(end-start)start = timer() X = X.astype(np.float64) Y = Y.astype(np.float64) X, Y = check_pairwise_arrays(X, Y) XX = row_norms(X, squared=True)[:, np.newaxis] YY = row_norms(Y, squared=True)[np.newaxis, :] distances = safe_sparse_dot(X, Y.T, dense_output=True) distances *= -2 distances += XX distances += YY distances = np.sqrt(distances) end = timer() print(end-start) print('') if abs(ans2 - distances) > 1e-3: # np.set_printoptions(precision=200) print(ans2) print(np.sqrt(distances)) print(X, Y) break—
You are receiving this because you were mentioned.
Reply to this email directly, view it on GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-337948154,
or mute the thread
https://github.com/notifications/unsubscribe-auth/AAEz6z5o2Ao_7V5-Lflb4HosMrHCeOrVks5st209gaJpZM4OXbpZ
.
anyway, would you like to submit a PR, @ragnerok?
yeah sure, what do you want me to do ?
provide a more stable implementation, also a test that would fail under the
current implementation, and ideally a benchmark that shows we do not lose
much from the change, in reasonable cases.
I wanted to ask if it is possible to find distance between each pair of rows with vectorisation. I cannot think about how to do it vectorised.
You mean difference (not distance) between pairs of rows? Sure you can do that if you're working with numpy arrays. If you have arrays with shapes (n_samples1, n_features) and (n_samples2, n_features), you just need to reshape it to (n_samples1, 1, n_features) and (1, n_samples2, n_features) and do the subtraction:
>>> X = np.random.randint(10, size=(10, 5))
>>> Y = np.random.randint(10, size=(11, 5))
X.reshape(-1, 1, X.shape[1]) - Y.reshape(1, -1, X.shape[1])
Yeah thanks that really helped 😄
I also wanted to ask if I provide a more stable implementation I won't be using X_norm_squared and Y_norm_squared. So do I remove them from the arguments as well or should I warn about it not being of any use ?
I think they will be deprecated, but we might need to first be assured that
there's no case where we should keep that version.
we're going to be quite careful in changing this. it's a widely used and
longstanding implementation. we should be sure not to slow any important
cases. we might need to do the operation in chunks to avoid high memory
usage (which is perhaps made trickier by the fact that this is called
within functions that chunk to minimise the output memory retirement from
pairwise distances).
I'd really like to hear from other core devs who know about computational
costs and numerical precision... @ogrisel, @lesteve, @rth...
On 5 Nov 2017 5:27 am, "Osaid Rehman Nasir" notifications@github.com
wrote:
I also wanted to ask if I provide a more stable implementation I won't be
using X_norm_squared and Y_norm_squared. So do I remove them from the
arguments as well or should I warn about it not being of any use ?—
You are receiving this because you were mentioned.
Reply to this email directly, view it on GitHub
https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-341919282,
or mute the thread
https://github.com/notifications/unsubscribe-auth/AAEz63izdpQGDEuW32m8Aob6rrsvV6q-ks5szKyHgaJpZM4OXbpZ
.
but it would be easier to discuss precisely if you open a PR
Ok I'll open up a PR then, with a very basic implementation of this function
The questions is what should be done about this for the 0.20 release. Could there be some simple / temporary improvements (event at the cost e.g. of memory usage) that could be considered?
The solution and analysis proposed in #11271 are definitely very valuable, but it might require some more discussion to make sure this is the optimal solution. In particular, I am concerned about the fact that now we have some pending discussion about the optimal global working memory in https://github.com/scikit-learn/scikit-learn/issues/11506 depending on the CPU type etc while this would add yet another level of chunking and the complexity of the whole would be getting a bit of control IMO. But maybe it's just me, looking for a second opinion.
What do you think should be done about this issue for the release @jnothman @amueller @ogrisel ?
Stability trumps efficiency. Stability issues should be fixed even when
efficiency still needs tweaks.
working_memory's focus was to make things like silhouette with large sample
sizes work. It also improved efficiency, but that can be tweaked down the
line.
I strongly believe we should try to get a fix for euclidean_distances with
float32 in. We broke it in 0.19 by assuming that we could make
euclidean_distances work on 32 bit in a naive way.
I agree that we need a fix. My concern here is not efficiency but the added complexity in the code base.
Taking a step back, scipy's euclidean implementation seems to be 10 lines of C code and for 32 bit, simply cast them to 64bit. I understand that it's not the fastest but it's conceptually easy to follow and understand. In scikit-learn, we use the trick to make computations faster in BLAS, then there are possible improvements due in https://github.com/scikit-learn/scikit-learn/pull/10212 and now the possible chunked solution to euclidean distance in 32 bit.
I'm just looking for input about what the general direction on this topic should be (e.g try to upstream some of it to scipy etc).
scipy doesn't seem concerned by copying the data...
Move to 0.21 following the PR.
Remove the blocker?
sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))
is numerically unstable, if dot(x,x) and dot(y,y) are of similar magnitude as dot(x,y) because of what is known as catastrophic cancellation.
This not only affect FP32 precision, but it is of course more prominent, and will fail much earlier.
Here is a simple test case that shows how bad this is even with double precision:
import numpy
from sklearn.metrics.pairwise import euclidean_distances
a = numpy.array([[100000001, 100000000]])
b = numpy.array([[100000000, 100000001]])
print "skelarn:", euclidean_distances(a, b)[0,0]
print "correct:", numpy.sqrt(numpy.sum((a-b)**2))
a = numpy.array([[10001, 10000]], numpy.float32)
b = numpy.array([[10000, 10001]], numpy.float32)
print "skelarn:", euclidean_distances(a, b)[0,0]
print "correct:", numpy.sqrt(numpy.sum((a-b)**2))
sklearn computes a distance of 0 here both times, rather than sqrt(2).
A discussion of the numerical issues for variance and covariance - and this trivially carries over to this approach of accelerating euclidean distance - can be found here:
Erich Schubert, and Michael Gertz.
Numerically Stable Parallel Computation of (Co-)Variance.
In: Proceedings of the 30th International Conference on Scientific and Statistical Database Management (SSDBM), Bolzano-Bozen, Italy. 2018, 10:1–10:12
Actually the y coordinate can be removed from that test case, the correct distance then trivially becomes 1. I made a pull request that triggers this numeric problem:
XA = np.array([[10000]], np.float32)
XB = np.array([[10001]], np.float32)
assert_equal(euclidean_distances(XA, XB)[0,0], 1)
I don't think my paper mentioned above provides a solution for this problem - just compute Euclidean distance as sqrt(sum(power())) and it is single-pass and has reasonable precision. The loss is in using the squares already, i.e., dot(x,x) itself already losing the precision.
@amueller as the problem may be more sever than expected, I suggest re-adding the blocker label...
Thanks for this very simple example.
The reason it is implemented this way is because it's way faster. See below:
x = np.random.random_sample((1000, 1000))
%timeit euclidean_distances(x,x)
20.6 ms ± 452 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
%timeit cdist(x,x)
695 ms ± 4.06 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Although the number of operations is of the same order in both methods (1.5x more in the second one), the speedup comes from the possibility to use well optimized BLAS libraries for matrix matrix multiplication.
This would be a huge slowdown for several estimators in scikit-learn.
Yes, but just 3-4 digits of precision with FP32, and 7-8 digits with FP64 does cause substantial imprecision, doesn't it? In particular, since such errors tend to amplify...
Well I'm not saying that it's fine right now. :)
I'm saying that we need to find a solution in between.
There is a PR (#11271) which proposes to cast on float64 to do the computations. In does not fix the problem for float64 but gives better precision for float32.
Do you have an example where using an estimator which uses euclidean_distances gives wrong results due to the loss of precision ?
I certainly still think this is a big deal and should be a blocker for 0.21. It was an issue introduced for 32 bit in 0.19, and it's not a nice state of affairs to leave. I wish we had resolved it earlier in 0.20, and I would be okay, or even keen, to see #11271 merged in the interim. The only issues in that PR that I know of surround optimisation of memory efficiency, which is a deep rabbit hole.
We've had this "fast" version for a long time, but always in float64. I know, @kno10, that it's got issues with precision. Do you have a good and fast heuristic for us to work out when that might be a problem and use a slower-but-surer solution?
Yes, but just 3-4 digits of precision with FP32, and 7-8 digits with FP64 does cause substantial imprecision, doesn't it
Thanks for illustrating this issue with very simple example!
I don't think the issue is as widespread as you suggest, however -- it mostly affects samples whose mutual distance small with respect to their norms.
The below figure illustrates this, for 2e6 random sample pairs, where each 1D samples is in the interval [-100, 100]. The relative error between the scikit-learn and scipy implementation is plotted as a function of the distance between samples, normalized by their L2 norms, i.e.,
d_norm(A, B) = d(A, B) / sqrt(‖A‖₂*‖B‖₂)
(not sure it's the right parametrization, but just to get results somewhat invariant to the data scale),
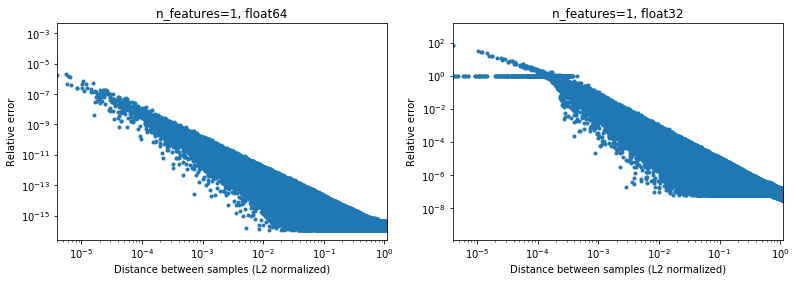
For instance,
- if one takes
[10000]and[10001]the L2 normalized distance is 1e-4 and the relative error on the distance calculation will be 1e-8 in 64 bit, and >1 in 32 bit (Or 1e-8 and >1 in absolute value respectively). In 32 bit this case is indeed quite terrible. - on the other hand for
[1]and[10001], the relative error will be ~1e-7 in 32 bit, or the maximum possible precision.
The question is how often the case 1. will happen in practice in ML applications.
Interestingly, if we go to 2D, again with a uniform random distribution, it will be difficult to find points that are very close,

Of course, in reality our data will not be uniformly sampled, but for any distribution because of the curse of dimensionality the distance between any two points will slowly converge to very similar values (different from 0) as the dimentionality increases. While it's a general ML issue, here it may mitigate somewhat this accuracy problem, even for relatively low dimensionality. Below the results for n_features=5,
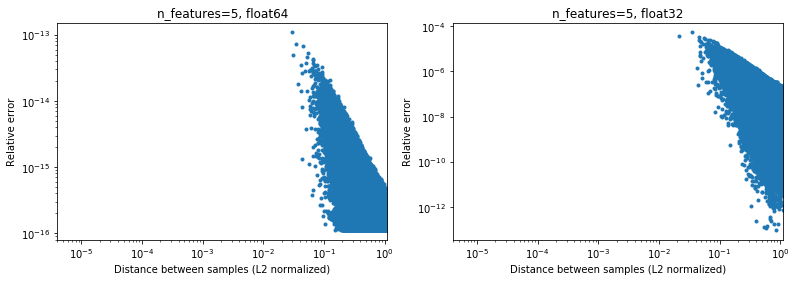 .
.
So for centered data, at least in 64 bit, it may not be so much of an issue in practice (assuming there are more then 2 features). The 50x computational speed-up (as illustrated above) may be worth it (in 64 bit). Of course one can always add 1e6 to some data normalized in [-1, 1] and say that the results are not accurate, but I would argue that the same applies to a number of numerical algorithms, and working with data expressed in the 6th significant digit is just looking for trouble.
(The code for the above figures can be found here).
Any fast approach using the dot(x,x)+dot(y,y)-2dot(x,y) version will likely have the same issue for all I can tell, but you'd better ask some real expert on numerics for this. I believe you'll need to double the precision of the dot products to get to approx. the precision of the *input data (and I'd assume that if a user provides float32 data, then they'll want float32 precision, with float64, they'll want float64 precision). You may be able to do this with some tricks (think of Kahan summation), but it will very likely cost you much more than you gained in the first place.
I can't tell how much overhead you get from converting float32 to float64 on the fly for using this approach. At least for float32, to my understanding, doing all the computations and storing the dot products as float64 should be fine.
IMHO, the performance gains (which are not exponential, just a constant factor) are not worth the loss in precision (which can bite you unexpectedly) and the proper way is to not use this problematic trick. It may, however, be well possible to further optimize code doing the "traditional" computation, for example to use AVX. Because sum( (x-y)*2 ) is all but difficult to implement in AVX.
At the minimum, I would suggest renaming the method to approximate_euclidean_distances, because of the sometimes low precision (which gets worse the closer two values are, which *may be fine initially then begin to matter when converging to some optimum), so that users are aware of this issue.
@rth thanks for the illustrations. But what if you are trying to optimize, e.g., x towards some optimum. Most likely the optimum will not be at zero (if it would always be your data center, life would be great), and eventually the deltas you are computing for gradients etc. may have some very small differences.
Similarly, in clustering, clusters will not all have their centers close to zero, but in particular with many clusters, x ≈ center with a few digits is quite possible.
Overall however, I agree this issue needs fixing. In any case we need to document the precision issues of the current implementation as soon as possible.
In general though I don't think the this discussion should happen in scikit-learn. Euclidean distance is used in various fields of scientific computing and IMO scipy mailing list or issues is a better place to discuss it: that community has also more experience with such numerical precision issues. In fact what we have here is a fast but somewhat approximate algorithm. We may have to implement some fixes workarounds in the short term, but in the long term it would be good to know that this will be contributed there.
For 32 bit, https://github.com/scikit-learn/scikit-learn/pull/11271 may indeed be a solution, I'm just not so keen of multiple levels of chunking all through the library as that increases code complexity, and want to make sure there is no better way around it.
Thanks for your response @kno10! (My above comments doesn't take it into account yet) I'll respond a bit later.
Yes, convergence to some point outside of the origin may be an issue.
IMHO, the performance gains (which are not exponential, just a constant factor) are not worth the loss in precision (which can bite you unexpectedly) and the proper way is to not use this problematic trick.
Well a >10x slow down for their calculation in 64 bit will have a very real effect on users.
It may, however, be well possible to further optimize code doing the "traditional" computation, for example to use AVX. Because sum( (x-y)**2 ) is all but difficult to implement in AVX.
Tried a quick naive implementation with numba (which should use SSE),
@numba.jit(nopython=True, fastmath=True)
def pairwise_distance_naive(A, B):
n_samples_a, n_features_a = A.shape
n_samples_b, n_features_b = B.shape
assert n_features_a == n_features_b
distance = np.empty((n_samples_a, n_samples_b), dtype=A.dtype)
for i in range(n_samples_a):
for j in range(n_samples_b):
psum = 0.0
for k in range(n_features_a):
psum += (A[i, k] - B[j, k])**2
distance[i, j] = math.sqrt(psum)
return distance
getting a similar speed to scipy cdist so far (but I'm not a numba expert), and also not sure about the effect of fastmath.
using the dot(x,x)+dot(y,y)-2*dot(x,y) version
Just for future reference, what we are currently doing is roughly the following (because there is a dimension that doesn't show in the above notation),
def quadratic_pairwise_distance(A, B):
A2 = np.einsum('ij,ij->i', A, A)
B2 = np.einsum('ij,ij->i', B, B)
return np.sqrt(A2[:, None] + B2[None, :] - 2*np.dot(A, B.T))
where both einsum and dot now use BLAS. I wonder, if aside from using BLAS, this also actually does the same number of mathematical operations as the first version above.
I wonder, if aside from using BLAS, this also actually does the same number of mathematical operations as the first version above.
No. The ((x - y)*2.sum()) performs
*n_samples_x * n_samples_y * n_features * (1 substraction + 1 addition + 1 multiplication)
whereas the x.x + y.y -2x.y performs
n_samples_x * n_samples_y * n_features * (1 addition + 1 multiplication).
There is a 2/3 ratio for the number of operations between the 2 versions.
Following the above discussion,
- Made a PR to optionally allow computing euclidean distances exactly https://github.com/scikit-learn/scikit-learn/pull/12136
- Some WIP to see if we can detect and mitigate the problematic points in https://github.com/scikit-learn/scikit-learn/pull/12142
For 32 bit, we still need to merge https://github.com/scikit-learn/scikit-learn/pull/11271 in some form though IMO, the above PRs are somewhat orthogonal to it.
FYI: when fixing some issues in OPTICS, and refreshing the test to use reference results from ELKI, these fail with metric="euclidean" but succeed with metric="minkowski". The numerical differences are large enough to cause a different processing order (just decreasing the threshold is not enough).
I'm really not caught up on this, but I'm surprised there's no existing solution. This seems to be a very common computation and it looks like we're reinventing the wheel. Has anyone tried reaching out to the wider scientific computing community?
Not yet, but I agree we should. The only thing I found about this in scipy was https://github.com/scipy/scipy/pull/2815 and linked issues.
I feel @jeremiedbb might have an idea?
Unfortunately not a satisfying one yet :(
We'd like to rely on a highly optimized library for this kind of computation, as we do for linear algebra with BLAS libraries such as OpenBLAS or MKL. But euclidean distance is not part of it. The dot trick is an attempt at doing that relying on BLAS level 3 matrix-matrix multiplication subroutine. But this is not precise and there is no way to make it more precise using the same method. We have to lower our expectancy either in term of speed or in term of precision.
I think in some situations, full precision is not mandatory and keeping the fast method is fine. This is when the distances are used for "find the closest" tasks. The precision issues in the fast method appear when the distances between points is small compared to their norm (in a ratio ~< 1e-4 for float 32 and ~< 1e-8 for float64). First for this situation to happen, the dataset needs to be quite dense. Then to have an ordering error, you need to have the two closest points within almost the same distance. Moreover, in that case, in a ML point of view, both would lead to almost equally good fits.
In the above situation, there is something we can do to lower the frequency of these wrong ordering (down to 0 ?). In the pairwise distance argmin situation. We can move the misordering to points which are not the closest. Essentially using the fact that one of the norm is not necessary to find the argmin, see comment. It has 2 advantages. It's a more robust (up to now I haven't found a wrong ordering yet) and it is even faster because it avoids some computations.
One drawback, still in the same situation, if at the end we want the actual distances to the closest points, the distances computed with the above method can't be used. They are only partially computed and they are not precise anyway. We need to re-compute the distances from each point to it's closest point. But this is fast because for each point there is only one distance to compute.
I wonder what I described above covers all the use case of euclidean_distances in sklearn. But I suggest to do that wherever it can be applied. To do that we can add a new parameter to euclidean_distances to only compute the necessary part in order to chain it with argmin. Then use it in pairwise_distances_argmin and in pairwise_distances_argmin_min (re computing the actual min distances at the end in the latter).
When we can't do that, fall back to the slow yet precise one, or add a switch like in #12136.
We can try to optimize it a bit to lower the performance drop cause I agree that this does not seem optimal. I have a few ideas for that.
Another possibility to keep using BLAS is combining axpy with nrm2 but this is far from optimal. Both are BLAS level 1 functions, and it involves a copy. This would only be faster in dimension > 100.
Ideally we'd like the euclidean distance to be included in BLAS...
Finally, there is another solution, consisting in upcasting. This is done in #11271 for float32. The advantage is that the speed is just half the current one and precision is kept. It does not solve the problem for float64 however. Maybe we can find a way to do a similar thing in cython for float64. I don't know exactly how but using 2 float64 numbers to kind of simulate a float128. I can give it a try to see if it's somewhat doable.
Ideally we'd like the euclidean distance to be included in BLAS...
Is that something the libraries would consider? If OpenBLAS does it we would be in a pretty good situation already...
Also, what's the exact differences between us doing it and the BLAS doing it? Detecting the CPU capabilities and deciding which implementation to use, or something like that? Or just having compiled versions for more diverse architectures?
Or just more time/energy spend writing efficient implementations?
This is interesting: an alternative implementation of the fast unstable method but claiming to be much faster than sklearn:
https://github.com/droyed/eucl_dist
(doesn't solve this issue at all though lol)
This discussion seems related https://github.com/scipy/scipy/issues/5657
Here's what julia does: https://github.com/JuliaStats/Distances.jl/blob/master/README.md#precision-for-euclidean-and-sqeuclidean
It allows setting a precision threshold to force recalculation.
Answering my own question: OpenBLAS has what looks like hand-written assembly for each processor (not architecture!) and heutistics to choose kernels for different problem sizes. So I don't think it's an issue of getting it into openblas as much as finding someone to write/optimize all those kernels...
Thanks for the additional thoughts!
In a partial response,
We'd like to rely on a highly optimized library for this kind of computation, as we do for linear algebra with BLAS libraries such as OpenBLAS or MKL.
Yeah, I also was hoping we could do more of this in BLAS. Last time I looked nothing in standard BLAS API looks close enough (but then I'm not an expert on those). BLIS might offer more flexibility but since we are not using it by default it's of somewhat limited use (though numpy might someday https://github.com/numpy/numpy/issues/7372)
Here's what julia does: It allows setting a precision threshold to force recalculation.
Great to know!
Should we open a separate issue for the faster approximate computation linked above? Seems interesting
Their speedup on CPU of x2-x4 might be due to https://github.com/scikit-learn/scikit-learn/pull/10212 .
I would rather open an issue on scipy once we have studied this question enough to come up with a reasonable solution there (and then possibly backport it) as I feel euclidean distance is something basic enough that should be of interest to many people outside of ML (and at the same time having the opinion of people there e.g. on accuracy issues would be helfpul).
It's up to 60x, right?
This is interesting: an alternative implementation of the fast unstable method but claiming to be much faster than sklearn
hum not sure about that. They are benchmarking %timeit pairwise_distances(a,b, 'sqeuclidean'), which uses scipy's one. They should do %timeit pairwise_distances(a,b, 'euclidean', metric_params={'squared': True}) and their speedup wouldn't be as good :)
As shown far earlier in the discussion, sklearn can be 35x faster than scipy
Yes, they benchmarks are only ~30% better better with metric="euclidean" (instead of squeclidean),
In [1]: from eucl_dist.cpu_dist import dist
... import numpy as np
In [4]: rng = np.random.RandomState(1)
... a = rng.rand(1000, 300)
...b = rng.rand(1000, 300)
In [7]: from sklearn.metrics.pairwise import pairwise_distances
In [8]: %timeit pairwise_distances(a, b, 'sqeuclidean')
214 ms ± 2.06 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
In [9]: %timeit pairwise_distances(a, b)
27.4 ms ± 2.48 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [10]: from eucl_dist.cpu_dist import dist
In [11]: %timeit dist(a, b, matmul='gemm', method='ext', precision='float32')
20.8 ms ± 330 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [12]: %timeit dist(a, b, matmul='gemm', method='ext', precision='float64')
20.4 ms ± 222 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
Is that something the libraries would consider? If OpenBLAS does it we would be in a pretty good situation already...
Doesn't sound straightforward. BLAS is a set of specs for linear algebra routines and there are several implementations of it. I don't know how open they are to adding new features not in the original specs. For that maybe blis would be more open but as said before, it's not the default for now.
Opened https://github.com/scikit-learn/scikit-learn/issues/12600 on the sqeuclidean vs euclidean handling in pairwise_distances.
I need some clarity about what we want for this. Do we want pairwise_distances to be close - in the sense of all_close - for both 'euclidean' and 'sqeuclidean' ?
It's a bit tricky. Because x is close to y does not mean x² is close to y². Precision is lost during squaring.
The julia workaround linked above is very interesting and is kind of straightforward to implement. However I suspect that it does not work as expected for 'sqeuclidean'. I suspect that you have to set the threshold way below to get the desired precision.
The issue with setting a very low threshold is that it induces a lot of re-computations and a huge drop of performances. However this is mitigated by the dimension of the dataset. The same threshold will trigger way less re-computations in high dimension (distances are bigger).
Maybe we can have 2 implementations and switch depending on the dimension of the dataset. The slow but safe one for low dimensional ones (there not much difference between scipy and sklearn in that case anyway) and the fast + threshold one for high dimensional ones.
This will need some benchmarks to find when to switch, and set the threshold but this may be a glimmer of hope :)
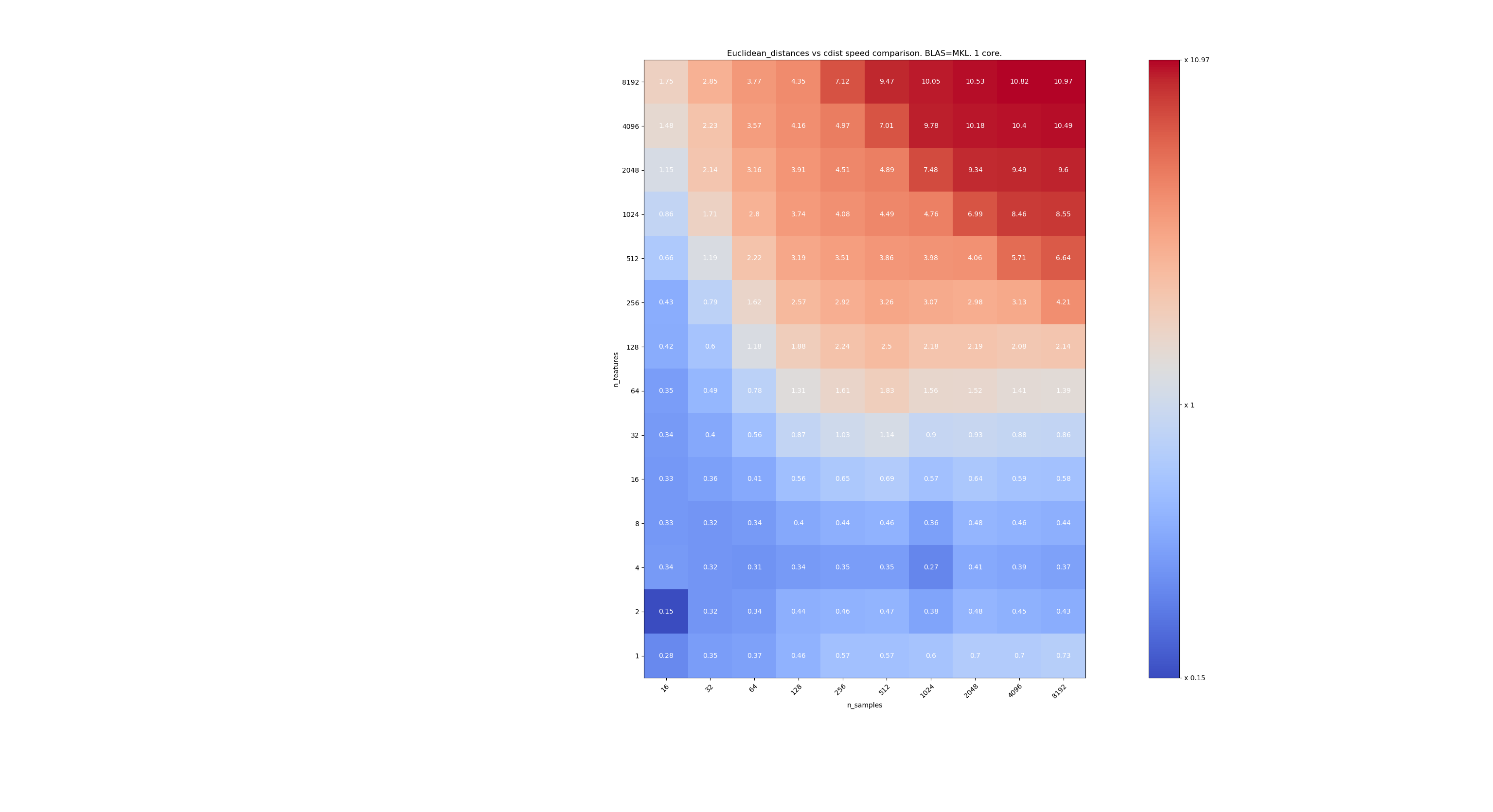
Here are some benchmarks for speed comparison between scipy and sklearn. The benchmarks compare sklearn.metrics.pairwise.euclidean_distances(X,X) with scipy.spatial.distance.cdist(X,X) for Xs of all sizes. Number of samples goes from 2⁴ (16) to 2¹³ (8192), and number of features goes from 2⁰ (1) to 2¹³ (8192).
The value in each cell is the speedup of sklearn vs scipy, i.e. below 1 sklearn is slower and above 1 sklearn is faster.
The first benchmark is using the MKL implementation of BLAS and a single core.
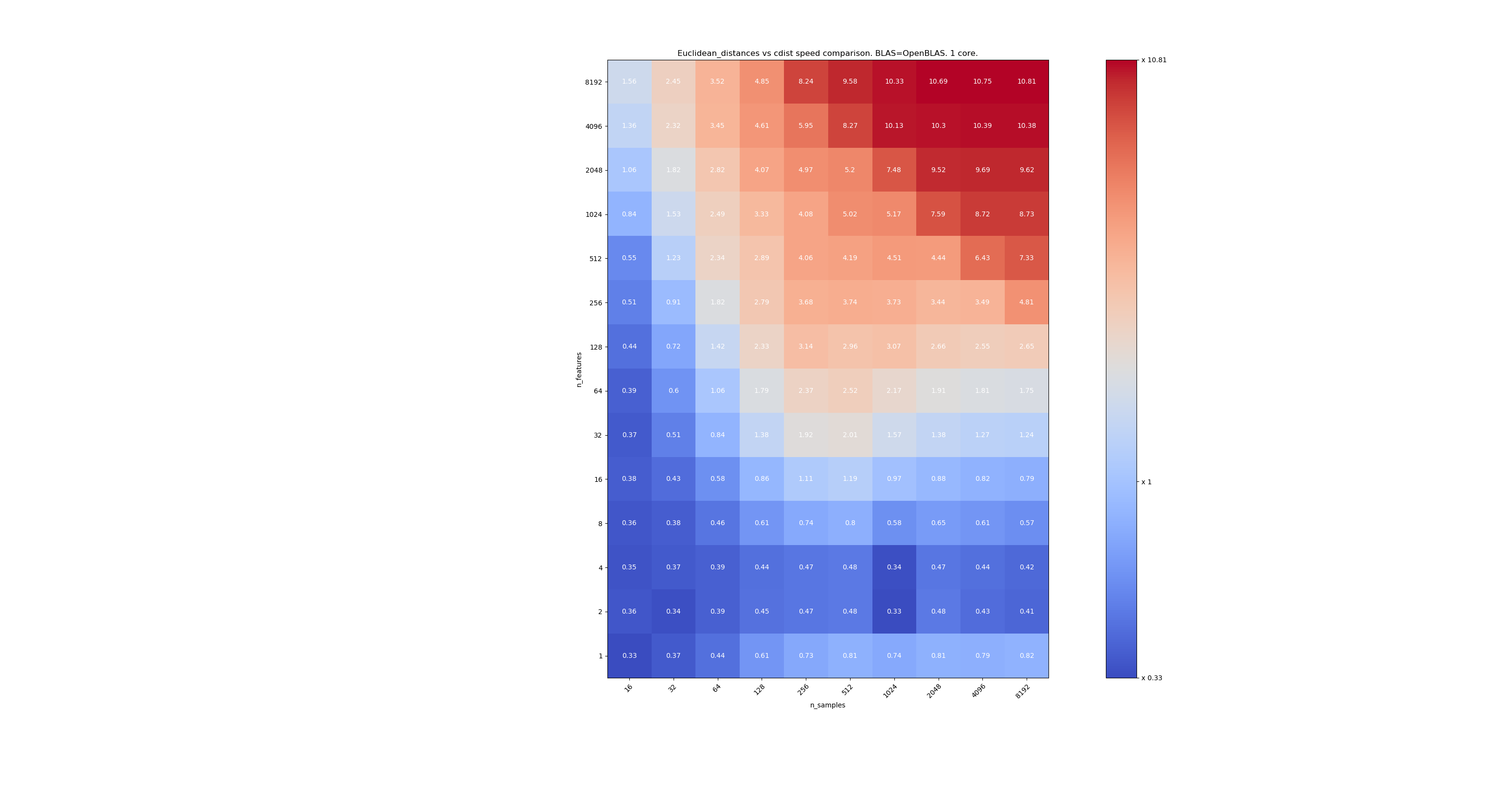
The second one is using the OpenBLAS implementation of BLAS and a single core. It's just to check that both MKL and OpenBLAS have the same behavior.
The third one is using the MKL implementation of BLAS and 4 cores. The thing is that euclidean_distances is parallelized through a BLAS LEVEL 3 function but cdist only uses a BLAS LEVEL 1 function. Interestingly it almost doesn't change the frontier.
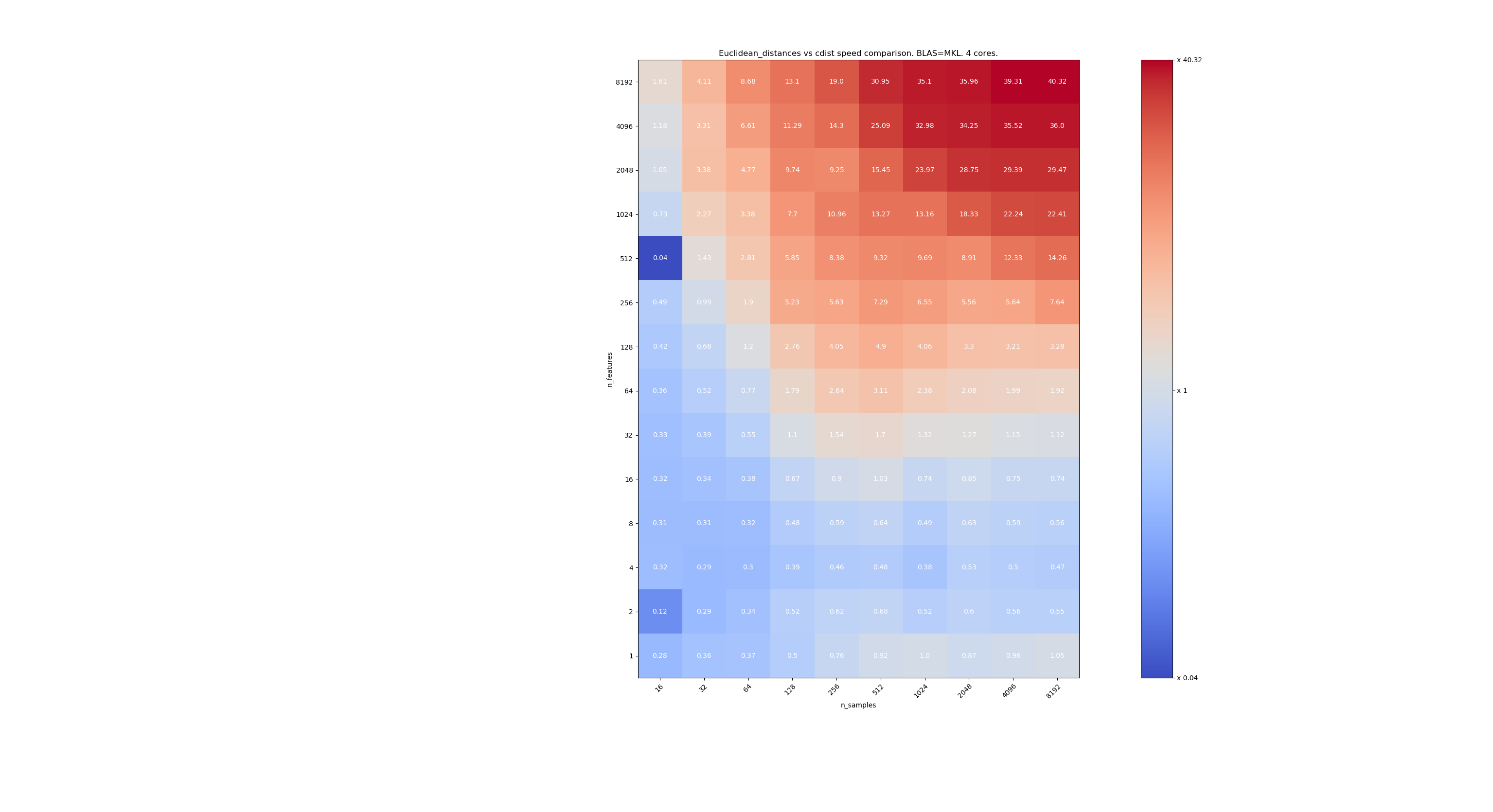
When n_samples is not too low (>100), it seems that the frontier is around 32 features. We could decide to use cdist when n_features < 32 and euclidean_distances when n_features > 32. This is faster and there no precision issue. This also has the advantage that when n_features is small, the julia threshold leads to a lot of re-computations. Using cdist avoids that.
When n_features > 32, we can keep the euclidean_distances implementation, updated with the julia threshold. Adding the threshold shouldn't slow euclidean_distances too much because the number of features is high enough so that only a few re-computations are necessary.
@jeremiedbb great, thank you for the analysis. The conclusion sounds like a great way forward to me.
Oh, I assume this was all for float64, right? What do we do with float32? upcast always? upcast for >32 features?
I've not read through the comments carefully (will soon), just FYI that float64 has it limitations, see #12128
@qinhanmin2014 yes, float64 precision has limitations, but it is precise enough for producing reliable fp32 results for all I can tell. The question is at which parameters an upcast to fp64 is actually cheaper than using cdist from scipy.
As seen in above benchmarks, even multi-core BLAS is not generally faster. This seems to mostly hold for high dimensional data (over 64 dimensions; before that the benefit is usually not worth the effort IMHO) - and since Euclidean distances are not that reliable in dense high dimensional data, that use case IMHO is not of highest importance. Many users will have less than 10 dimensions. In these cases, cdist seems to usually be faster?
Oh, I assume this was all for float64, right?
Actually it's for both float32 and float64 (I mean very similar). I suggest to always use cdist when n_features < 32.
The question is at which parameters an upcast to fp64 is actually cheaper than using cdist from scipy.
Upcasting will slowdown by a factor of ~2 so I guess around n_features=64.
Many users will have less than 10 dimensions.
But not everyone, so we still need to find a solution for high dimensional data.
Very nice analysis @jeremiedbb !
For low dimensional data it would definitely make sense to use cdist then.
Also, FYI scipy's cdist upcasts float32 to float64 https://github.com/scipy/scipy/issues/8771#issuecomment-384015674, I'm not sure if this is due to accuracy issues or something else.
Overall, I think it could make sense to add the "algorithm" parameter to euclidean_distance as suggested in https://github.com/scikit-learn/scikit-learn/pull/12601#pullrequestreview-176076355, possibly with a default to "None" so that it could also be set via a global option as in https://github.com/scikit-learn/scikit-learn/pull/12136.
There's also an interesting approach in Eigen3 to compute stable norms: https://eigen.tuxfamily.org/dox/StableNorm_8h_source.html (that I haven't really grokked yet)
Good Explanation, Improved my understanding
We haven't made any progress on this at the sprint and we probably should... and @rth is not around today.
I can join remotely if you set a time. Maybe in the beginning of afternoon?
To summarize the situation,
For precision issues in Euclidean distance calculations,
- in the low dimensional case, as @jeremiedbb showed above, we should probably use cdist
- in the high dimensional case and float32, we could choose between,
- chunking, computing the distance in 64 bit and concatenating
- falling back to cdist in cases when precision is an issue (how is an open question -- reaching out e.g. to scipy might be useful https://github.com/scikit-learn/scikit-learn/issues/9354#issuecomment-438522881 )
Then there are all the issues of inconsistencies between euclidean, sqeuclidean, minkowski, etc.
In terms of the precisions, @jeremiedbb, @amueller and I had a quick chat, mostly just milking Jeremie for his expertise. He is of the opinion that we don't need to worry so much about the instability issues in an ML context in high dimensions in float64. Jeremie also implied that it is hard to find an efficient test for whether good results have been returned (cf. #12142)
So I think we're happy with @rth's preceding comment with the upcasting for float32. Since cdist also upcasts to float64, we could reimplement cdist to take float32 (but with float64 accumulators?), or could use chunking, if we want less copying in low-dim float32.
Does @Celelibi want to change the PR in #11271, or should someone else (one of us?) produce a complete pull request?
And once this has been fixed, I think we should make sqeuclidean and minkowski(p in {0,1}) use our implementations. We've not discussed discrepancy with NearestNeighbors. Another sprint :)
After a quick discussion at the sprint we ended up on the following way:
in high dimensional case (> 32 or > 64 choose the best): upcast by chunks to float64 when it's float32 and keep the 'fast' method. For this kind of data, numerical issues, on float64, are almost negligible (I'll provide benchmarks for that)
in low dimensional case: implement the safe computation (instead of using scipy cdist because of the upcast) in sklearn.
(It's tempting to throw upcasting float32 into 0.20.3 also)
Here are some benchmarks for speed comparison between scipy and sklearn.
[... snip ...]
This is very interesting. I wasn't actually expecting this result. I re-did your benchmark and found a very similar result. Except I would advocate for a lower decision boundary. My benchmark would suggest 8 features.

The cost of being wrong is not symmetric. cdist is better only for computations lasting less than a few seconds and it gets slow really fast when the number of feature increase. So, better use the BLAS implementation when in doubt.
Edit: This benchmark was for float64, but I also find that upcasting float32 matrices to float64 only barely add a few percent to the total time and doesn't change the conclusion.
I noticed that the threshold depends on the machine you're running the benchmarks on. I suspect it may have to do with the AVX instructions. I realized the benchmarks I published were run on a machine which didn't have AVX2 instructions, only AVX. And on a machine which have AVX2, I got similar results to yours.
But the question is not only about performance but also about precision and it's more likely to have precision issues when the dimension is small. Maybe 16 is a good compromise. What do you think ?
In regards of this discussion, I'd say we need to benchmark the accuracy to take an informed decision.
However, in regards of your PR, the accuracy shouldn't be an issue anymore. But at the cost of a slightly more expensive computation. Therefore the threshold should probably be decided by benchmarking your PR.
Benchmarking accuracy is not that easy. Because the difficult cases will not be uniformly distributed.
And it may be problematic if it happens undetected in a corner case. Usually, you will want to have guaranteed numerical accuracy within affordable CPU limits.
But as mentioned elsewhere a single feature with 10000000.01 and 10000000.00 should be enough to trigger numeric instability with fp64 when using the known-problematic equation, 10000 and 10001 with fp32. With 1024 features, try
>>> import sklearn.metrics.pairwise as sk, scipy.spatial.distance as sp
>>> X = [[10000.01] * 1024, [10000.00] * 1024]
>>> print(sk.euclidean_distances(X,X), "\n", sp.cdist(X,X))
[[ 0. 0.31895195]
[ 0.31895195 0. ]]
[[ 0. 0.32]
[ 0.32 0. ]]
(this was using 0.19.1) The correct distance is 0.32.
As you can see, the numeric instabilities tend to get worse with the number of features (unless your data is sparse). Here, the result has less than two digits of precision with FP64.
13410 does not fix this specific case. i.e float64 + high dimension.
It fixes it for float32 however.
But we decided that for float64 + high dim, we keep it as it was, because the accuracy issues are very unlikely to happen and don't really apply to machine learning use cases.
In your example, X[0] and X[1] have norms equal to 320000.32 and 320000 and their distance is 0.32, i.e. 1e-6 times their norm. In machine learning, the 16 significant digits (in float64) are not all relevant.
But we decided that for float64 + high dim, we keep it as it was, because the accuracy issues are very unlikely to happen and don't really apply to machine learning use cases.
I would be more moderate on this one. Reducing the dimensionality is a usual first step in ML. MDS can be used for that, and it makes a heavy use of the euclidean distance matrix.
If someone want to have a look at improving the accuracy of the float64 case, there's a way to use two floats to represent the intermediate results. Although I think it starts to fall beyond the scope of scikit-learn.
ftp://ftp.math.ethz.ch/users/wpp/CELL/qd.pdf
I was not clear. I'm not saying high dimensional data does not apply to machine learning. I'm saying that the kind of precision issues which happen in float64 involves points which distance is 6 orders of magnitude smaller than their norms. Having such a precision has no meaning in a realistic machine learning model
In machine learning, the 16 significant digits (in float64) are not all relevant.
I am not at all convinced that this is that generally true.
In this example, we have lost 15 of 16 digits in precision. I'd agree if we would use half of the precision, but we don't have such a relationship. The loss from downcasting FP64 to FP32 may often be tolerable because of measurement precision. And consumer-grade GPUs are much faster with FP32 than with FP64, for example (in some cases, they allow FP32 data and FP64 accumulators now, though), and for neural networks inference, you may even see int8 now. But that doesn't hold everywhere.
For example in k-means clustering, there is the assumption that clusters differ substantially in their means (and that we don't know the means beforehand), and hence we have a loss in precision here. If you have many clusters, some of their norms can be large compared to their separation.
Furthermore, after the first initial iterations, its often small differences in distance that make one point switch to another cluster. Loss of precision here can affect results, and could cause instability.
Now consider k-means on time series fragments with many variables.
With increasing data sizes, we must assume that the distances to the nearest neighbor get smaller, and unless your norms are 0, they will eventually be smaller than the vector norms and cause problems. So this will likely become more severe with increasing data set sizes. The curse of dimensionality says that the largest and the smallest distances get more and more similar; so in order to compute the correct nearest neighbor ranking, we may need good precision in high-dimensional data. On the 20news data set, the smallest non-zero distance is around 0.02 (the norms are all 1). But that is just 10k instances, and fairly diverse contents. Now assume the data set was about near-duplicate detection instead...
I would not be sure this "unlikely" happens in ML... of course it won't affect everybody though.
When I say "In machine learning, the 16 significant digits (in float64) are not all relevant.", I'm not speaking of the computed distance, I'm speaking of the data X.
In machine learning, your data comes from a measure, and there's no measure precise to the 9th digit (besides very few ones in particle physics).
So in your example of 10000000.01 and 10000000.00, how would you give some importance to a distance of 0.01 when your uncertainty on the values of X are way bigger ?
For KMeans, first there's a way to overcome a large part of losses of precision. When you're looking for the closest center of an observation x, you don't need to add the norm of x to the distance calculation which avoids the catastrophic cancellation in most cases.
Then, kmeans clusters based on euclidean distances. But you don't know if this is the exact way your data are gathered. In fact there's a 0 probability that your data is clustered that way. Kmeans gives an estimation of how your data could be clustered and points which are at the frontier of 2 clusters can definitely not be considered belonging with certainty to one or the other. What's your interpretation of a point at the same distance of 2 clusters ? Mine is either the 2 clusters should be only one cluster or KMeans is not the best algo to cluster my data (or even kmeans gives me a somewhat good idea of how my data is clustered but I know that frontiers of clusters are not relevant).
The use of only "|b|^2-2ab" does not have catastrophic cancellation - but the same loss in precision in the digits that make the difference. The results are the same as if you added the norm of a to each distance afterwards; if the distances are much smaller than the norm of a, then you get a loss in precision that is avoidable by doing the computations the traditional way without BLAS hacks.
So you actually can NOT overcome the numerical problem this way!
K-means is an optimization problem. So such hacks may mean that sklearn finds only worse solutions than other tools. And as indicated before, this can also cause instabilities. In the worst case, this could cause sklearn kmeans to iterate through the same states until max_iter with no improvement (assuming tol=0, if you want to find a local optimum), which theory would say is impossible.
Until k-means has converged, you can't say much about points with the "same" distance to two clusters. The next iteration, the means may have moved and the difference could become much larger and matter!
I am not a big fan of k-means because it doesn't work too well on noisy data. But there are variations that handle such cases better. But nevertheless, if you use it, you should probably try to get the full quality (which is why I also always use tol=0) and not make it worse than necessary. It's cheap enough to do the proper calculations (and, as mentioned, the problems get worse with data size - so for small data, the slower runtime does usually not matter, for larger data sets the precision becomes more likely important).
Depending on the application, the difference between 10000000.01 and 10000000.00 can matter. And as I showed before, if you use multiple features the problems arise earlier. With fp32 as little as 10000 and 10001 with a single feature and 100 vs. 101 with 100 features I guess:
As mentioned, the mean may have a physical meaning that you don't want to lose. If you have data with temperatures in Kelvin, you don't want to 0:1 scale them or center them; that would ruin your ratio scale. Now if you want to compare, for example, time series of the temperature of some steel product as it cools down, and figure out if the cool down process affects the reliability of your steel product. You may be having temperatures of over 700 K, and the time series may have hundreds of data points if you want to analyze the cooldown process. Even with just 5 digits of input precision (0.01K) with the length of the time series the numeric problem can occur. You may again end up with only 1-2 digits in the result. I don't think you can just rule out that precision ever matters in ML if you have this catastrophic kind of effect. Its a different if you could guarantee to always get, say 10 of 16 digits in precision. Here you can't do that, you may have 0 digits right in the worst case (that is why it's catastrophic).
In machine learning, your data comes from a measure, and there's no measure precise to the 9th digit (besides very few ones in particle physics).
The raw values from the real world rarely have that kind of accuracy, that's right. But ML isn't limited to that kind of input. One might want to apply ML to mathematical problems, like applying MDS on the graph of a rubik's cube-like puzzle or clustering the successful strategies found by your swarm of RL agents playing pacman.
Even if the initial source of the information is the real world, there might be some mid-way processing that makes most digits relevant to the clustering algorithm. Like the result of a gradient descent on a function whose parameters are statistically sampled in the real world.
I'm actually wondering why we're still discussing this. I guess we all agree that scikit-learn should try its best in the trade-off accuracy vs. computation time. And whoever isn't happy with the current state should submit a pull request.
The use of only "|b|^2-2ab" does not have catastrophic cancellation - but the same loss in precision in the digits that make the difference. The results are the same as if you added the norm of a to each distance afterwards; if the distances are much smaller than the norm of a, then you get a loss in precision that is avoidable by doing the computations the traditional way without BLAS hacks.
So you actually can NOT overcome the numerical problem this way!
There is a loss of precision, but it can't cause a catastrophic cancellation (at least when a and b are close), and you can show that the relative error on the distance (which is not a distance) stays small.
In the case of KMeans where you're only interested in finding the closest center, you have enough precision to keep the ordering right. If at the end you want the inertia, then you can just calculate the distances of each point to its cluster center with the exact formula.
Besides, KMeans is not a convex optimization problem, so even if you let it run with tol=0 until convergence, you end up in a local minima which can be far off the global minima (even with kmeans++ initialization). So I'd rather run kmeans many times with different init and a reasonably small number of iterations. You'll have better chance to end up in a better local minima. Then you can rerun the best one until convergence.
The relative error compared to the real distance can be arbitrary large, and hence cause wrong nearest neighbors. Consider the case where |a|²=|b|²=1, for example on tf-idf. Assume that the vectors are very close. Then ab is also close to 1, and at this point you already lost much of your precision.
As I wrote above, the error is there, even if you don't have catastrophic cancellation. Consider 8 digits of precision. The real distance may be 0.000012345678 and can be computed with eight digits using FP32 and regular Euclidean distance. But with this equation, you compute the value ab=0.99998765432 instead, which with FP32 will be truncated to approximately 0.99998765 at best, so you lost three digits of precision unnecessarily in this example. The loss is as big as in the catastrophic case. If the distances are much smaller than the norms, your precision can become arbitrarily bad with this approach.
Yes, kmeans is not convex. But then you will want to at least find a local optimum, and not get stuck (or even oscillate because the resulting errors behave erratically) because your precision is too low. So you at least get a chance to find the global one in well-behaved cases and with multiple attempts.
I appreciate this discussion, but what we really need is a solution that is no worse than what we were doing before we stopped upcasting things to float64. In that sense, @Celelibi's upcasting solution was sufficient. Using the exact solution in low dimensions is an added improvement on what we used to do.
Regarding a future version, do you feel any more confidence to efficiently detect when we might consider the exact computation in high dimensions?
I've run a benchmark to evaluate the average accuracy of the float64 case with random numbers. I compare 3 algorithms: neumaier_sum((x-y)**2), numpy.sum((x-y)**2) and X2 - 2*X.dot(Y.T) + Y2.T. The exact result to compare to has been obtained using mpmath with a precision of 256 bits.
X and Y have 100 samples and a variable number of features and are filled with random numbers between -2 and 2.
On the following gif, there's one image per number of feature (between 1 and 200). On each image, each dot represent the relative error of the squared euclidean distance between one of the 10000 pair of vectors of X and Y. The relative error is multiplied by 2^53 for readability, which corresponds roughly to the ULP unit.
The curves above are the approximate distribution (using a kernel density estimate).

Note that the graphs were cut at 6 ULP for readability. It shows the average case, not the worse case. The error of the expanded formula can grow pretty large.
My analysis of this result is that on average, the relative error of the expanded formula can be very large with few features, but quickly become similar to that of the difference and numpy sum. The threshold being between 5 and 10 features.
I'm also currently trying to find an upper bound for the error of the expanded formula as well as pathological examples.
I think @kno10's concern is that we are often interested in cases where
points are not randomly distributed, but are near each other or have unit
norm.
Indeed, but I needed to be convinced that in practice, it's not complete BS. ^^
To complete the comment above: the relative error of the formula x²+y²-2ab seems to be unbounded. Unless my analysis is wrong, when x and y are close to each other, the relative error can be up to 2^(52*2). At least theoretically. In practice, the worst case I found is a relative error of 2^52+1.
>>> a, b = (0xfffffec4d6282+1) * 2.0**(511-52), 0xfffffec4d6282 * 2.0**(511-52)
>>> a, b
(6.703903473040778e+153, 6.7039034730407766e+153)
>>> exactdiff = (a-b)**2
>>> exactdiff
2.2158278651204453e+276
>>> computeddiff = a**2 + b**2 - 2*a*b
>>> computeddiff
-9.9792015476736e+291
>>> abs((computeddiff - exactdiff) / exactdiff)
4503599627370497.0
>>> bin(int(abs((computeddiff - exactdiff) / exactdiff)))
'0b10000000000000000000000000000000000000000000000000001'
Flipping the sign of the result would actually make it closer to the truth. This is the most dramatic example I could find, but actually changing the exponent in the values of a and b doesn't change the relative error.
>>> a, b = (0xfffffec4d6282+1) * 2.0**(-52), 0xfffffec4d6282 * 2.0**(-52)
>>> a, b
(0.9999999266202912, 0.999999926620291)
>>> exactdiff = (a-b)**2
>>> computeddiff = a**2 + b**2 - 2*a*b
>>> abs((computeddiff - exactdiff) / exactdiff)
4503599627370497.0
I think a histogram plot in ULPs would make more sense than above animation with the within-ULP error distribution. So 0 ULP error and 1 ULP error are "as good as it gets". 2 ULP is likely unavoidable because of the sqrt. Any larger errors are worth investigating I assume.
Using (computed - exact) / exact is reasonable as long as exact is large. But once we are getting numerical challenges for the exact value, this becomes quite unstable. In such cases, (computed-exact)/norm may be worth using instead, i.e. looking at the precision of our distance computations compared to the input data, not compared to the derived distances.
If we have two one-dimensional values that only differ by 1 ULP, and error of 2 ULP may seem huge; but we are at input data resolution already, so the results are quite unstable.
Note that with multiple dimensions, we may get a higher resolution in the input data.
Consider input data of the type (1, 1e-16) vs. (1, 2e-16). For example if we have a constant attribute in the input data, say, a white pixel in MNIST.
With the difference-based equation this will be fine, but the dot-version gets into trouble, doesn't it? That is why one-dimensional experiments may not be enough to study this.
I think a histogram plot in ULPs would make more sense than above animation with the within-ULP error distribution.
I'm not sure I see how you would have represented it. There would be one histogram per number of feature and per algorithm. There's not much I can do beside a 3D plot or an animation.
Using
(computed - exact) / exactis reasonable as long as exact is large. But once we are getting numerical challenges for the exact value, this becomes quite unstable.
I'm not sure what you mean by unstable in this context. The exact value should be computed with whatever it takes to make it exact.
(Speaking of which, I should have computed the relative error with arbitrary precision too in my plot, instead of comparing to the exactly rounded result. I updated my plot, the weird waves disappeared.)
In such cases,
(computed-exact)/normmay be worth using instead, i.e. looking at the precision of our distance computations compared to the input data, not compared to the derived distances.
If I understand your idea correctly, you would rather compare the absolute error to the magnitude of the input data. Using the vector norms as an aggregated measure of the magnitude of the inputs. Whereas the standard relative error compare it to the magnitude of the exact result.
I think with this metric you try to capture how much faulty is an algorithm. But it actually doesn't seem particularly useful for a few reasons.
- It doesn't really say how many digits of the result are inexact.
- Actually, most algorithms would have a score less than 1e-15. Even the expanded formula (dot-based algorithm) would have a score bounded by something like 5 ULP(input) (rough estimation, I didn't write the full proof).
- And since both metrics are just a rescaled version of the absolute error
computed - exact, they would rank the algorithms in the same order when evaluated on the same inputs.
So it's the same as the usual relative error, just with a value interpretation less useful (IMO).
Consider input data of the type
(1, 1e-16)vs.(1, 2e-16). For example if we have a constant attribute in the input data, say, a white pixel in MNIST.
With the difference-based equation this will be fine, but the dot-version gets into trouble, doesn't it? That is why one-dimensional experiments may not be enough to study this.
The dot-based algorithm would have a relative error of 1, meaning that the error is as large as the exact result, and thus, no digit of the result is correct. And your metric would have a value of 1e-16 meaning that relative to the scale of the vector norm, only the 16th digit is off.
I'm unsure what you're trying to show with this example.
If we are still concerned about the precision of euclidean_distances with float64, probably better to summarize this discussion in a new issue as there are 100 comments here.
Most helpful comment
The raw values from the real world rarely have that kind of accuracy, that's right. But ML isn't limited to that kind of input. One might want to apply ML to mathematical problems, like applying MDS on the graph of a rubik's cube-like puzzle or clustering the successful strategies found by your swarm of RL agents playing pacman.
Even if the initial source of the information is the real world, there might be some mid-way processing that makes most digits relevant to the clustering algorithm. Like the result of a gradient descent on a function whose parameters are statistically sampled in the real world.
I'm actually wondering why we're still discussing this. I guess we all agree that scikit-learn should try its best in the trade-off accuracy vs. computation time. And whoever isn't happy with the current state should submit a pull request.