Runtime: Different algorithm result on different OS

[enricobenedos]

Issue Title

Good Morning,

I've a .NET CORE API hosted on a Linux environment. My develop machine is a macOS. In both cases I'm using .NET CORE SDK/Runtime 3.1.
The same code executed on my machine works perfectly but on the Linux environment it generate an exception when trying to convert a decimal number

System.OverflowException: Value was either too large or too small for a Decimal.
at System.Number.ThrowOverflowException(TypeCode type)
at System.Decimal.DecCalc.VarDecFromR8(Double input, DecCalc& result)
at WamiiApi.Controllers.ToursController.PostTours(Tours tours) in /home/wamii/wamii_api_v2/WamiiApi/Controllers/ToursController.cs:line 156
at lambda_method(Closure , Object )
at Microsoft.AspNetCore.Mvc.Infrastructure.ActionMethodExecutor.AwaitableObjectResultExecutor.Execute(IActionResultTypeMapper mapper, ObjectMethodExecutor executor, Object controller, Object[] arguments)

The problem seems not related directly to decimal conversion but from a my own open source library code execution.
When calling GetDistance method different result with the same parsed file are returned:

• Nan on Linux
• No sense number on Windows
• Correct number on macOS

```c#
public double GetDistance()
{
List latitudesXAtt = gpx.XPathSelectElements("//p:gpx//p:trk//p:trkseg//p:trkpt", xmlNamespaceManager).Attributes("lat").ToList();
List longitudesXAtt = gpx.XPathSelectElements("//p:gpx//p:trk//p:trkseg//p:trkpt", xmlNamespaceManager).Attributes("lon").ToList();

        double dist = 0.0;
        for (int i = 0; i < latitudesXAtt.Count - 1; i++)
        {
            double lat1 = double.Parse(latitudesXAtt[i].Value);
            double lat2 = double.Parse(latitudesXAtt[i + 1].Value);

            double lon1 = double.Parse(longitudesXAtt[i].Value);
            double lon2 = double.Parse(longitudesXAtt[i + 1].Value);

            double rlat1 = Math.PI * lat1 / 180;
            double rlat2 = Math.PI * lat2 / 180;
            double theta = lon1 - lon2;
            double rtheta = Math.PI * theta / 180;
            double distance =
               Math.Sin(rlat1) * Math.Sin(rlat2) + Math.Cos(rlat1) *
               Math.Cos(rlat2) * Math.Cos(rtheta);
            distance = Math.Acos(distance);
            distance = distance * 180 / Math.PI;

            dist += distance * 60 * 1.1515;
        }

        return dist * 1.609344;
    }

```

At the moment I do not have a sample file to provide you. But I'm not able to understand why the same file with the same algorithm can return different results.

Can anyone help me to understand why same code return different results on different platforms?

Thanks

[Dotnet-GitSync-Bot]

I couldn't figure out the best area label to add to this issue. If you have write-permissions please help me learn by adding exactly one area label.

[scalablecory]

CC @tannergooding

[msftbot[bot]]

Tagging subscribers to this area: @tannergooding, @pgovind
See info in area-owners.md if you want to be subscribed.

[am11]

Unrelated to the platform disparity; I think that method needs if (lat1 == lat2 && lon1 == lon2) continue; after double lon2 = double.Parse(longitudesXAtt[i + 1].Value); line.

tested your code on macOS and Ubuntu with one complex gpx file, Math.Acos turns 1.000003 like numbers into NaN. I also cannot share the file; company property etc. 😉

[andrea5586]

Recalling from high school, you can pass to acos function values between -1 and 1. This is proved by the documentation
https://docs.microsoft.com/en-us/dotnet/api/system.math.acos?view=netcore-3.1

If the parameter passed to acos is outside the range (-1,1). NaN is returned.

Still doesn't explain the different result based on the platform.

[am11]

If the parameter passed to acos is outside the range (-1,1). NaN is returned.

The way this method is written (iteratively) this can happen in realworld valid GPX file. That's why we need the early bail.

[enricobenedos]

@am11 thank for the code improvement about the algorithm (if (lat1 == lat2 && lon1 == lon2) continue;). But the problem in this case is not related to some equals points.
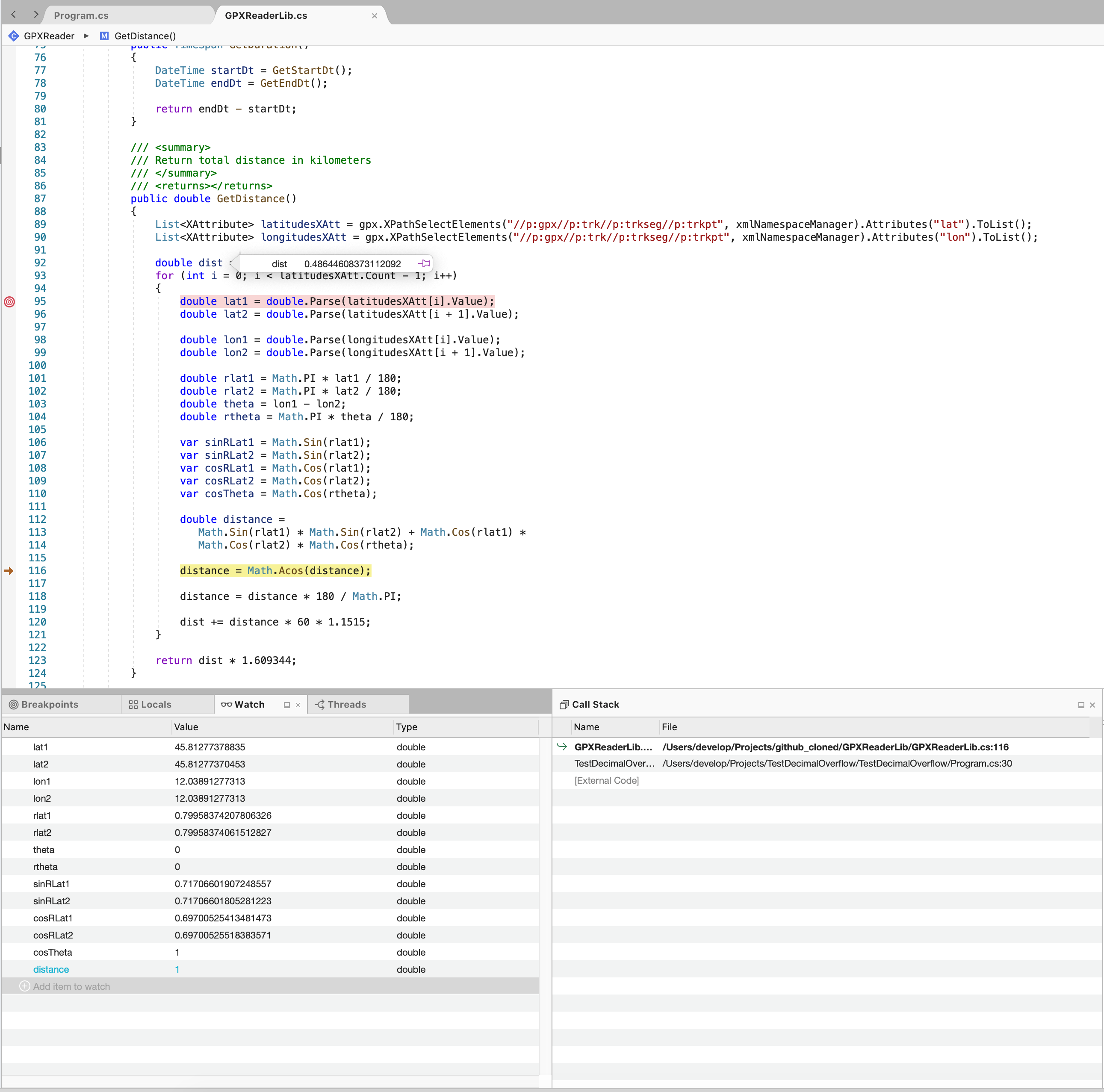
Now I'm able to show you that there is a platform problem related to Math.Sin method that show why on macOS there are no problem differently from linux.

Same code and same input vars on both OS as you can see from the screenshots

• On macOS distance value is 1 and then the acos method can return a correct value
  

• On linux distance value is not 1 but 1.00000....02
  

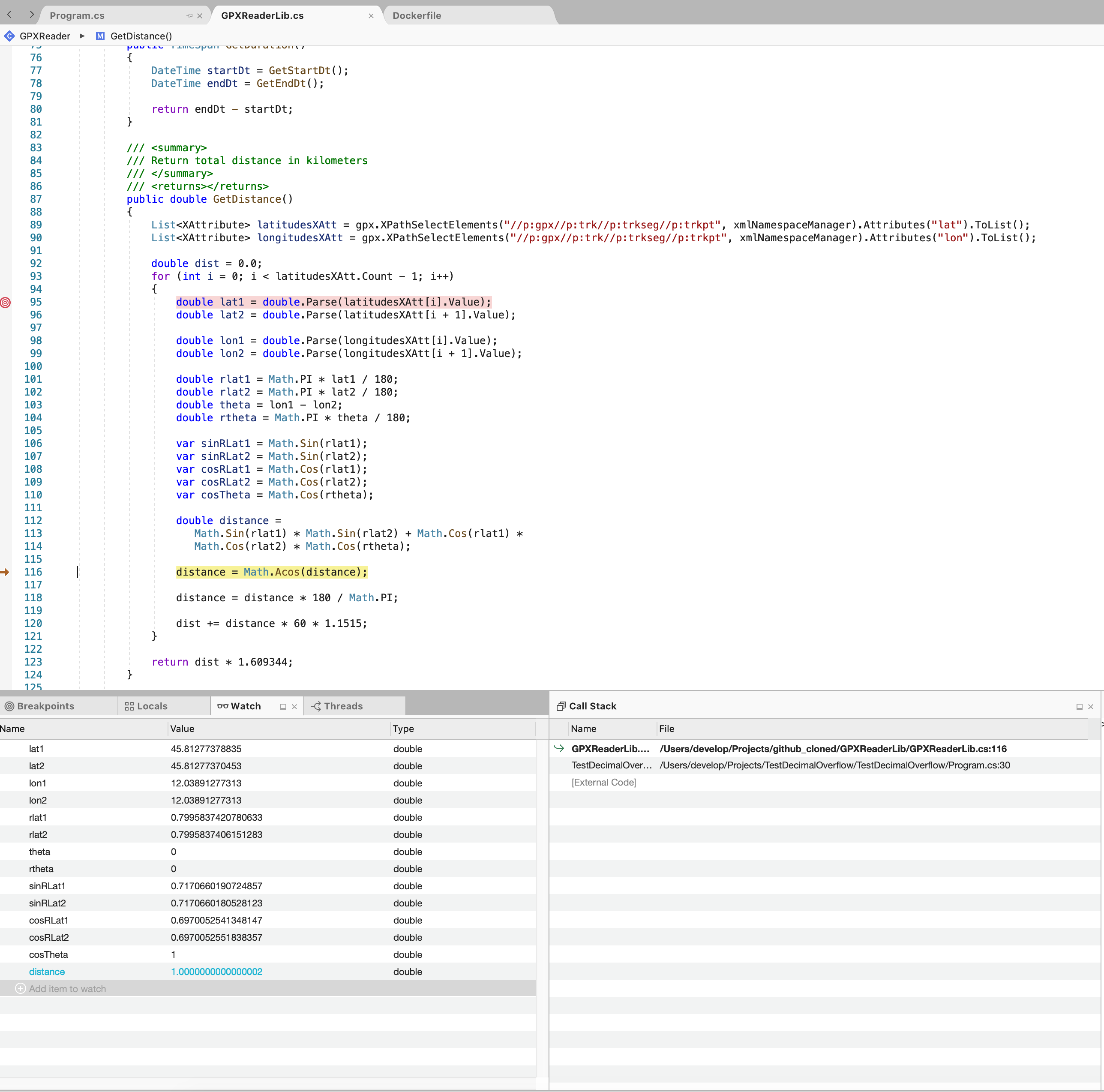
Seems that on Linux operations results\values are rounded differently from Mac in which I have one more decimal value.

Can anyone can explain me this issue? It is very strange and on my humble opinion there is something wrong!

[am11]

Thanks for the screenshot. A self-contained repro, without library would be:

c# class Program { static void Main() => System.Console.WriteLine(System.Math.Sin(0.7995837420780633)); }

Linux: 0.7170660190724857
macOS: 0.7170660190724856

This is by the language specification: https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/language-specification/types

The double type can represent values ranging from approximately 5.0 * 10^-324 to 1.7 × 10^308 with a precision of 15-16 digits.

So I think it is best to define an epsilon value withing that range and ignore the least significant digits for distance calculation.

[tannergooding]

This is by the language specification: https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/language-specification/types

This is misleading at best. While you need no more than 17 digits to produce a roundtrippable string, the underlying float/double may have significantly more digits available.
The longest float actually has 112 digits while the longest double has 767 digits, when looking at the exact value represented.

When calling GetDistance method different result with the same parsed file are returned

The issue here is in the underlying implementations for the various Math functions. Simple operations, such as +, -, *, /, and % are deterministic and will always produce the same result on all platforms, as per the IEEE 754 specification.
However, due to a number of factors the Math functions are currently implemented as invocations down into the corresponding C Runtime implementations. That is MathF.Cos calls into std::cosf, for example.

Each platform/architecture (so MacOS, Windows, Linux; but also x86 vs x64 vs ARM32 vs ARM64, and all the variations there-of) currently has a different underlying implementation which can result in minor differences in the computed result. These differences can be more extreme at the input edges and can become more extreme as the errors build up over the course of many operations.

There is currently a work item on my plate to investigate resolving this issue, either by reimplementing the algorithms in managed code or by finding a common implementation we can use in C/C++. However, this is a large undertaking due to the complexity of the underlying algorithms, the risk of introducing regressions (either in computed result or perf), and the need for a large amount of investigatory work to show the benefits/drawbacks of each possible solution.

As it is currently, the differences are "by design" and are no different then you would compute when comparing native implementations written in C/C++ or many other languages that also rely on the underlying C Runtime implementation.

[tannergooding]

CC. @jeffhandley, here is another example of where normalizing the Math implementations would help resolve customer bugs/issues.

[enricobenedos]

Thank you @am11 for the Microsoft documentation snippet.
But at this point which "parameter" decides the precision value? Who decides to use 15 instead of 16 digit?
At this point every time I need to write a boiler plate on my code that fix the number of digits in order to have a standard length. But it is crazy because I'm using a cross platform framework in order to avoid differences between OS.
(The answer is in @tannergooding post)

Thank you @tannergooding! Your explanation was what I'm looking for.

However, due to a number of factors the Math functions are currently implemented as invocations down into the corresponding C Runtime implementations. That is MathF.Cos calls into std::cosf, for example.
Each platform/architecture (so MacOS, Windows, Linux; but also x86 vs x64 vs ARM32 vs ARM64, and all the variations there-of) currently has a different underlying implementation which can result in minor differences in the computed result. These differences can be more extreme at the input edges and can become more extreme as the errors build up over the course of many operations.

Hope that Microsoft team will find a solution about that. In my own small I understand that it is not simple.
Anyway I will fix my code writing something that cut numbers to 14 digits hoping that in future this issue will be solved because debugging has not sense on different OS than the production one (and it can create a lot of confusion).

[tannergooding]

It's not quite as simple as just cutting digits.

float and double (and now Half) are binary-based floating-point numbers. This means they work a bit differently from normal "decimal" arithmetic you may be used to.

Namely, they are constructed out of a 1-bit sign, x-bit exponent, and y-bit mantissa. For float, there are 8-exponent bits and 24 mantissa bits (one of which is implicitly determined based on the exponent), while double has an 11-bit exponent, and 53-bit mantissa (also with one bit being implicitly determined). You combine these values as -1^sign * 2^exponent * mantissa to compute the exact value that is represented.

One of the things that this means is that values that aren't a power of 2 or a multiple of a power of 2 cannot be exactly represented. So while 1, 2, 4, etc and 0.5, 0.25, 0.125, etc can all be exactly represented; a value like 0.1 cannot, instead when you do double x = 0.1 it is rounded to the nearest representable result, which is 0.1000000000000000055511151231257827021181583404541015625.

Due to the underlying representation, the distance between representable values also changes every power of 2. For example, the distance between 0.25 (2^-2) and the smallest value that is greater than 0.25 is 5.5511151231257827021181583404541015625E-17 and this delta is used for all values between 0.25 and 0.5 inclusive. Once you hit 0.5 (2^-1) that delta doubles to 1.1102230246251565404236316680908203125E-16 and is the new distance for all values between 0.5 and 1.0, inclusive. Once you hit 1.0 (2^0), it doubles again to 2.220446049250313080847263336181640625E-16 for all values between 1.0 and 2.0, etc.

This means that the smallest value less than 0.1 (which is exactly represented as 0.1000000000000000055511151231257827021181583404541015625) is 0.09999999999999999167332731531132594682276248931884765625 and the smallest value greater than 0.1 is 0.10000000000000001942890293094023945741355419158935546875. Values in between these ranges will get rounded to whichever of the three is the nearest representable.

These differences between the literal value given in code and the actual value represented also means that there are minor inaccuracies produced in any floating-point code written, which may introduce other errors in the final result produced. The most common example is that (0.1 + 0.2) == 0.3 will print false. This is because 0.1 is 0.1000000000000000055511151231257827021181583404541015625, 0.2 is 0.200000000000000011102230246251565404236316680908203125, and 0.3 is 0.299999999999999988897769753748434595763683319091796875. While 0.1 + 0.2 is 0.3000000000000000444089209850062616169452667236328125. If you compare the values there, you'll find that 0.299999999999999988897769753748434595763683319091796875 is closer to 0.3 than 0.3000000000000000444089209850062616169452667236328125 is, which is why it is chosen and that the inaccuracies introduced by 0.1 and 0.2 not being exactly representable produce 0.3000000000000000166533453693773481063544750213623046875, which is closer to 0.3000000000000000444089209850062616169452667236328125.

What all this ultimately means is that you may have to perform additional analysis on the inputs/outputs of the algorithm and account for these rounding errors. It also means that you may have to take into account that the math, which is binary based, may not produce exactly the same result as you might expect from "decimal based" arithmetic and normal shortcuts may not work as expected or apply exactly the same.

This is also true, to an extent, for any math computed where the results are limited to a finite space. You can run into similar rounding issues with decimal as well, for example, but may find things work more "naturally" (how you are used to) most of the time with it being base-10, rather than base-2.

[andrea5586]

Thank you @tannergooding for your time to give us this complete explanation: this is a matter @enricobenedos and I where discussing, but couldn't relate to the platform disparity.

We will for sure keep in mind this concepts.

[tannergooding]

Happy to answer any other questions, but closing this for now since the behavior is expected/by-design for now.