Nim: [Perf] Max/min are not inline and slow (7x slower than memory-bound implementation)

[mratsim]

Context

While implementing high-performance computing kernels and checking kadro library by @bluenote10, I noticed that he tried to optimize Nim max implementation. I also benchmarked it and there a huge function call overhead in the current implementation in system.nim. See also https://github.com/bluenote10/kadro/issues/2#issuecomment-433047530. This also part of the cause of Arraymancer perf issues mentioned by @andreaferretti in https://github.com/mratsim/Arraymancer/issues/265.

The relu operation is basically max(0, x) and is a staple in Neural Networks and can be applied repeatedly on tensors of hundreds of millions of parameters:

# This is a simple image recognition neural net
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 20, 5)
        self.conv2 = nn.Conv2d(20, 50, 5)
        self.linear1 = nn.Linear(800, 500)
        self.linear2 = nn.Linear(500, 10)

    def forward(self, x):
        batch_size, _, _, _ = x.size()
        x = self.conv1(x)
        x = F.relu(F.max_pool2d(x, 2)) # <------ max(0, x)
        x = self.conv2(x)
        x = F.relu(F.max_pool2d(x, 2)) # <------ max(0, x)
        x = x.view(batch_size, 800)
        x = F.relu(self.linear1(x)) # <------ max(0, x)
        x = self.linear2(x)
        return x

Benchmark results

Benchmark is done on i5-5257U 2.7Ghz turbo 3.1 of Broadwell generation from a macBook Pro 2015

I benchmarked Nim system, an "inline max" which is just a copy paste with inline, and a SSE3 implementation which bottlenecks on how fast you can retrieve data from memory for the theoretical maximum throughput.

Let's start with the results

Only -d:release

Warmup: 1.2016 s, result 224 (displayed to avoid compiler optimizing warmup away)

Reduction - system.nim - max - float32
Collected 1000 samples in 20.024 seconds
Average time: 20.020 ms
Stddev  time: 0.605 ms
Min     time: 19.646 ms
Max     time: 24.334 ms
Theoretical perf: 499.507 MFLOP/s

Display max of samples maxes to make sure it's not optimized away
0.9999996423721313

Reduction - inline max - max - float32
Collected 1000 samples in 20.252 seconds
Average time: 20.248 ms
Stddev  time: 0.271 ms
Min     time: 19.648 ms
Max     time: 23.316 ms
Theoretical perf: 493.876 MFLOP/s

Display max of samples maxes to make sure it's not optimized away
0.9999996423721313

Reduction - SSE3 max mem bandwidth - max - float32
Collected 1000 samples in 2.748 seconds
Average time: 2.744 ms
Stddev  time: 0.244 ms
Min     time: 2.348 ms
Max     time: 5.597 ms
Theoretical perf: 3643.700 MFLOP/s

Display max of samples maxes to make sure it's not optimized away
0.9999996423721313

-d:release + march=native + fastmath

Warmup: 1.1972 s, result 224 (displayed to avoid compiler optimizing warmup away)

Reduction - system.nim - max - float32
Collected 1000 samples in 16.826 seconds
Average time: 16.821 ms
Stddev  time: 0.555 ms
Min     time: 16.567 ms
Max     time: 23.897 ms
Theoretical perf: 594.483 MFLOP/s

Display max of samples maxes to make sure it's not optimized away
0.9999996423721313

Reduction - inline max - max - float32
Collected 1000 samples in 2.654 seconds
Average time: 2.650 ms
Stddev  time: 0.212 ms
Min     time: 2.445 ms
Max     time: 4.833 ms
Theoretical perf: 3773.566 MFLOP/s

Display max of samples maxes to make sure it's not optimized away
0.9999996423721313

Reduction - SSE3 max mem bandwidth - max - float32
Collected 1000 samples in 2.558 seconds
Average time: 2.554 ms
Stddev  time: 0.240 ms
Min     time: 2.331 ms
Max     time: 5.381 ms
Theoretical perf: 3915.447 MFLOP/s

Display max of samples maxes to make sure it's not optimized away
0.9999996423721313

You can see that the inline_max reaches 95% of the throughput of my SSE3 kernel.

What is happening

Some ASM info, functions suffixed by ss work on scalar like maxss, functions suffixed by ps work on a vector of 4xfloat32 like maxps. ss pour scalar single opposed to sd for scalar double and ps for packed single as opposed to pd for packed double.

system.nim max:

Notice how when going from release to release + fastmath + march-native the complex "max" function is simplified to vmaxss, however the loop cannot be simplified because max is not inline. LTO would probably work as an alternative at the expense of slower compile-time.

You can also see that in the fastmath max you have 1 instruction that do work vmaxss and the rest is just bookkeeping.

Loop - release only

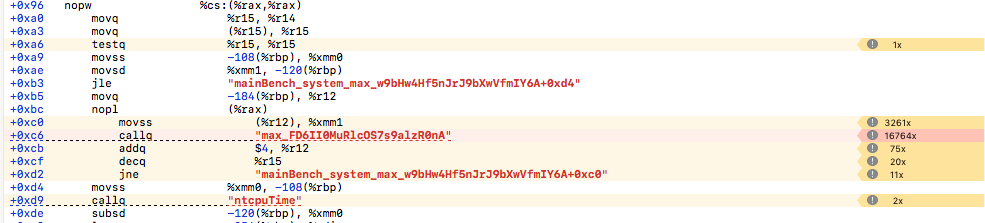
Max - release only

Loop - release + march=native + fast-math

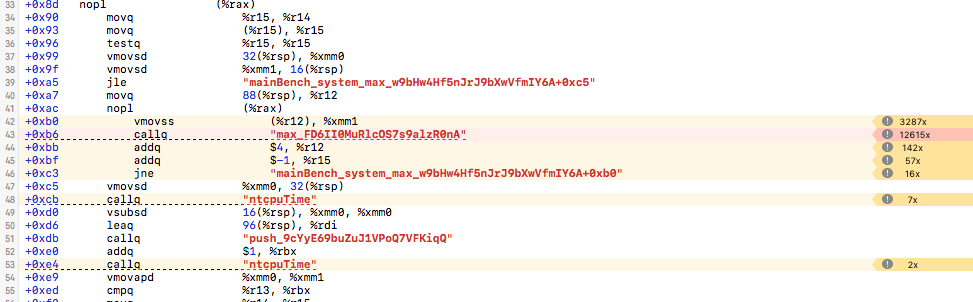
Max - release + march=native + fast-math

1 instruction doing work, 5 doing bookkeeping

inline.nim max:

When the function is inline, fast-math + march-native make the compiler recognize the max function and vectorization opportunities, it even uses the 32-byte wide AVX instead of 16-byte wide SSE, though that doesn't really improve speed compared to pure SSE due to the memory bottleneck.

Loop & inline Max - release only

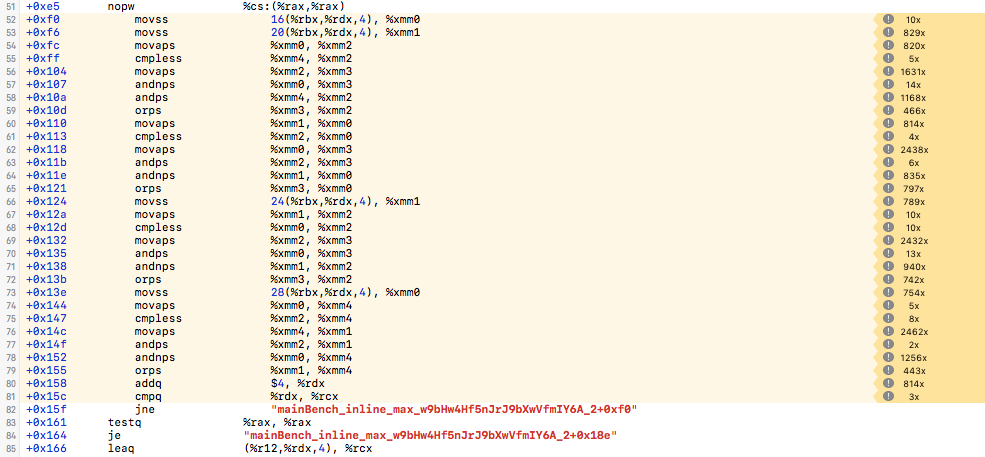
Loop & inline Max - release + march=native + fastmath

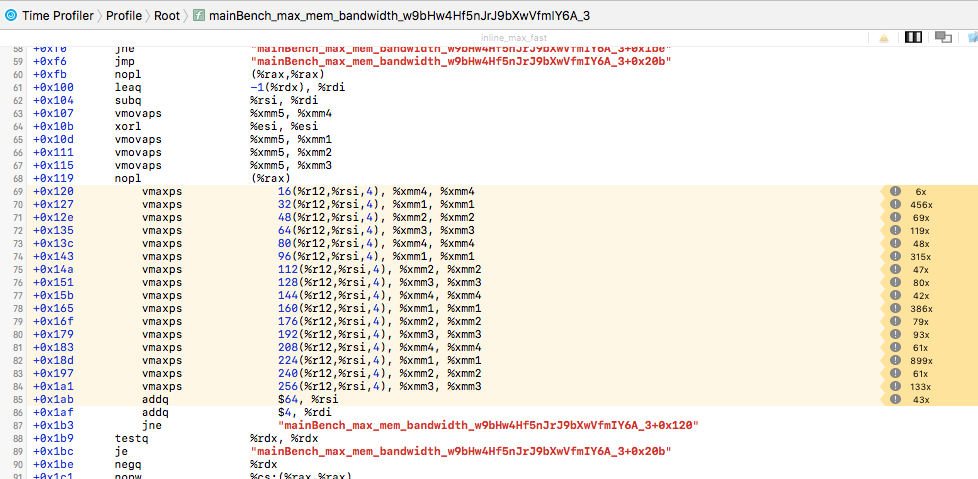
Optimized SSE3 max:

Release only:

Notice the sudden increase of perf counter which means that we are hitting a memory bottleneck

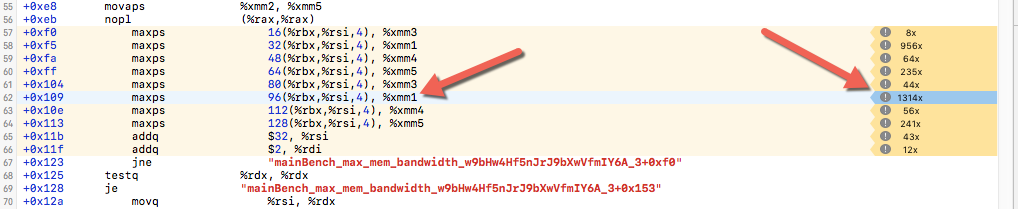
Release + fastmath:

Request:

max and min function should be inline and similar small functions in system.nim/math.nim should be {.inline.} as well.

This will allow the compiler to recognize vectorization opportunities.

Furthermore, with full optimizations turned on, you can see that the max function becomes 1 "work" instruction and 5 booking instructions that push or retq.

Reproduction code

# ##########################################
# Benchmarking tools
import random, times, stats, strformat, math, sequtils

proc warmup() =
  # Warmup - make sure cpu is on max perf
  let start = cpuTime()
  var foo = 123
  for i in 0 ..< 300_000_000:
    foo += i*i mod 456
    foo = foo mod 789

  # Compiler shouldn't optimize away the results as cpuTime rely on sideeffects
  let stop = cpuTime()
  echo &"Warmup: {stop - start:>4.4f} s, result {foo} (displayed to avoid compiler optimizing warmup away)"

template printStats(name: string, accum: float32) {.dirty.} =
  echo "\n" & name & " - float32"
  echo &"Collected {stats.n} samples in {global_stop - global_start:>4.3f} seconds"
  echo &"Average time: {stats.mean * 1000 :>4.3f} ms"
  echo &"Stddev  time: {stats.standardDeviationS * 1000 :>4.3f} ms"
  echo &"Min     time: {stats.min * 1000 :>4.3f} ms"
  echo &"Max     time: {stats.max * 1000 :>4.3f} ms"
  echo &"Theoretical perf: {a.len.float / (float(10^6) * stats.mean):>4.3f} MFLOP/s"
  echo "\nDisplay max of samples maxes to make sure it's not optimized away"
  echo accum # Prevents compiler from optimizing stuff away

template bench(name: string, accum: var float32, body: untyped) {.dirty.}=
  block: # Actual bench
    var stats: RunningStat
    let global_start = cpuTime()
    for _ in 0 ..< nb_samples:
      let start = cpuTime()
      body
      let stop = cpuTime()
      stats.push stop - start
    let global_stop = cpuTime()
    printStats(name, accum)

# #############################################

func inline_max[T](x, y: T): T {.inline.}=
  if y <= x: x else: y

# #############################################
# SIMD

when defined(vcc):
  {.pragma: x86_type, byCopy, header:"<intrin.h>".}
  {.pragma: x86, noDecl, header:"<intrin.h>".}
else:
  {.pragma: x86_type, byCopy, header:"<x86intrin.h>".}
  {.pragma: x86, noDecl, header:"<x86intrin.h>".}
type
  m128* {.importc: "__m128", x86_type.} = object
    f0, f1, f2, f3: float32

## SSE1
func mm_set1_ps*(a: float32): m128 {.importc: "_mm_set1_ps", x86.}
  ## [a, a, a, a]
func mm_load_ps*(aligned_data: ptr float32): m128 {.importc: "_mm_load_ps", x86.}
  ## Load 4 packed float32 in __m128. They must be aligned on 16-byte boundary.
func mm_load_ss*(aligned_data: ptr float32): m128 {.importc: "_mm_load_ss", x86.}
  ## Load 1 float32 in __m128. in the lower word and zero the rest.
func mm_max_ps*(a, b: m128): m128 {.importc: "_mm_max_ps", x86.}
  ## Vector maximum
func mm_max_ss*(a, b: m128): m128 {.importc: "_mm_max_ss", x86.}
  ## Low part max + copy of a
  ## Input:
  ##   { A0, A1, A2, A3 }, { B0, B1, B2, B3 }
  ## Result:
  ##   { max(A0,B0), A1, A2, A3 }

## SSE3
func mm_movehdup_ps*(a: m128): m128 {.importc: "_mm_movehdup_ps", x86.}
  ## Duplicates high parts of the input
  ## Input:
  ##   { A0, A1, A2, A3 }
  ## Result:
  ##   { A1, A1, A3, A3 }
func mm_movehl_ps*(a, b: m128): m128 {.importc: "_mm_movehl_ps", x86.}
  ## Input:
  ##   { A0, A1, A2, A3 }, { B0, B1, B2, B3 }
  ## Result:
  ##   { B2, B3, A2, A3 }
func mm_cvtss_f32*(a: m128): float32 {.importc: "_mm_cvtss_f32", x86.}
  ## Extract the low part of the input
  ## Input:
  ##   { A0, A1, A2, A3 }
  ## Result:
  ##   A0
# #############################################

func round_step_down*(x: Natural, step: static Natural): int {.inline.} =
  ## Round the input to the previous multiple of "step"
  when (step and (step - 1)) == 0:
    # Step is a power of 2. (If compiler cannot prove that x>0 it does not make the optim)
    result = x and not(step - 1)
  else:
    result = x - x mod step

func merge_max_vec_sse3*(vec: m128): m128 {.inline.}=
  ## Reduce packed packed 4xfloat32
  let shuf = mm_movehdup_ps(vec)
  let sums = mm_max_ps(vec, shuf)
  let shuf2 = mm_movehl_ps(sums, sums)
  result = mm_max_ss(sums, shuf2)

func max_sse3*(data: ptr UncheckedArray[float32], len: Natural): float32 =
    ## Sum a contiguous range of float32 using SSE3 instructions
    let data = data
    var vec_result = mm_set1_ps(float32(-Inf))

    # Loop peeling, while not aligned to 16-byte boundary advance
    var idx = 0
    while (cast[ByteAddress](data) and 15) != 0:
      let data0 = data[idx].addr.mm_load_ss()
      vec_result = mm_max_ss(vec_result, data0)
      inc idx

    let data_aligned = cast[ptr UncheckedArray[float32]](data[idx].addr)

    # Main vectorized and unrolled loop.
    const step = 16
    let new_end = len - idx
    let unroll_stop = round_step_down(new_end, step)
    var
      accum4_0 = mm_set1_ps(float32(-Inf))
      accum4_1 = mm_set1_ps(float32(-Inf))
      accum4_2 = mm_set1_ps(float32(-Inf))
      accum4_3 = mm_set1_ps(float32(-Inf))

    for i in countup(0, unroll_stop - 1, step):
      let
        data4_0 = data_aligned[i   ].addr.mm_load_ps()
        data4_1 = data_aligned[i+4 ].addr.mm_load_ps()
        data4_2 = data_aligned[i+8 ].addr.mm_load_ps()
        data4_3 = data_aligned[i+12].addr.mm_load_ps()
      accum4_0 = mm_max_ps(accum4_0, data4_0)
      accum4_1 = mm_max_ps(accum4_1, data4_1)
      accum4_2 = mm_max_ps(accum4_2, data4_2)
      accum4_3 = mm_max_ps(accum4_3, data4_3)
    accum4_0 = mm_max_ps(accum4_0, accum4_1)
    accum4_2 = mm_max_ps(accum4_2, accum4_3)
    accum4_0 = mm_max_ps(accum4_0, accum4_2)

    for i in unroll_stop ..< new_end:
      let data0 = data_aligned[i].addr.mm_load_ss()
      vec_result = mm_max_ss(vec_result, data0)
    vec_result = mm_max_ss(vec_result, accum4_0.merge_max_vec_sse3())
    result = vec_result.mm_cvtss_f32()

# #############################################

proc mainBench_system_max(a: seq[float32], nb_samples: int) =
  var accum = float32(-Inf)
  bench("Reduction - system.nim - max", accum):
    for i in 0 ..< a.len:
      accum = max(accum, a[i])

proc mainBench_inline_max(a: seq[float32], nb_samples: int) =
  var accum = float32(-Inf)
  bench("Reduction - inline max - max", accum):
    for i in 0 ..< a.len:
      accum = inline_max(accum, a[i])

proc mainBench_max_mem_bandwidth(a: seq[float32], nb_samples: int) =
  var accum = float32(-Inf)
  bench("Reduction - SSE3 max mem bandwidth - max", accum):
    accum = max_sse3(cast[ptr UncheckedArray[float32]](a[0].unsafeAddr), a.len)

# ###############################################

when defined(fastmath):
  {.passC:"-ffast-math".}

when defined(march_native):
  {.passC:"-march=native".}

when isMainModule:
  randomize(42) # For reproducibility
  warmup()
  block:
    let
      a = newSeqWith(10_000_000, rand(-1.0'f32 .. 1.0'f32))
    mainBench_system_max(a, 1000)
    mainBench_inline_max(a, 1000)
    mainBench_max_mem_bandwidth(a, 1000)

[Clyybber]

@mratsim I just want to say that I love the way you present your issues/bug reports. It's always a joy to read through some of the longer/deeper ones.

[Araq]

This is excellent information but a PR that adds .inline to min/max would have been less work. :-)

[mratsim]

I already did the work anyway to investigate the slowness so ;)

[dom96]

Perhaps it would worth turning this into a blog post? :)