Marlin: [bugfix-1.1.x] Using thermistor table 71 fails to compile

[agrif]

Description

Compiling Marlin on the latest bugfix-1.1.x (ccb225f43ae76dee1eada30b88004352a19a7134) fails when it is configured to use thermistor table 71, with a static assertion:

thermistortables.h:207: error: static assertion failed: Temperature conversion tables over 127 entries need special consideration.

From discussion in this commit and this follow-up commit, it looks like this is a static assert to guard against an overflow in [temperature.cpp:928][].

@thinkyhead, you mentioned that no temperature table has more than 128 entries. Am I counting wrong? It looks like thermistor 71 has about 140 entries.

It seems this could be fixed for up to 256 entries, at the cost of an extra subtraction, by replacing [temperature.cpp:928][] with:

m = l + ((r - l) >> 1);

Steps to Reproduce

1. Set TEMP_SENSOR_0 (or any other thermometer) to 71
2. Attempt to compile.

Expected behavior: Successful compilation.

Actual behavior: Failed compilation.

Additional Information

I have zipped my configuration files, in case that is useful.

[AnHardt]

Instead of slowing down 500*analog sensors using a table, per second, it makes more sense to me, to speed up table 71 by cutting out every second value. This will not lose much exactness of the results (I guess less than 0.1K).

EDIT
Or simply cut away the linear parts of the tabe - like lines 39-58. The used linear interpolation will exactly replace all this values without any error

EDIT2
Table lookup is done only about 5 times / sensor / second because the other interrupts are needed for oversampling.

[agrif]

I'm not opposed to reducing the number of entries, but I thought the whole point of using a binary search was to allow for more points in a table.

I'm no AVR wizard, but that for loop looks like 20+ cycles per iteration easy. Adding an 8-bit subtraction to that loop will, at absolute worst, add 5% to the call time. 8-bit SUB is a 1-cycle instruction.

Edit: not to be too grumpy, but you all changed a linear algorithm to a logarithmic one, and broke things along the way. I think you can afford a single cycle to fix it.

[AnHardt]

... I thought the whole point of using a binary search was to allow for more points in a table.

The won time can be invested in two ways. Either in having more time, for example to better fill the planner buffer, or in having more points in the table it this results in a better temperature curve.

If we have a linear interpolation in between the points we have the table could have only two entries if the curve would be linear and steady. Usually thermistors don't have a linear curve but this curve is steady (has no jumps in it). By having more points in the table we can better approximate the shape of the curve by a sequence of steady lines but steadynes suffers. If the points are too close together and the values are integers we get a steppy curve.
So table 71 is broken by design.

For sure binary search is faster for a random temperature. But usually our target temperatures used to be relative close to the max temperatures of the tables, only a few entries away from the end. So in this special case linear search could be faster (at least when putting some brain into the tables and stopping to believe: more is better ).

[agrif]

I've gone and plotted table 71, just so we can all see what we're talking about:

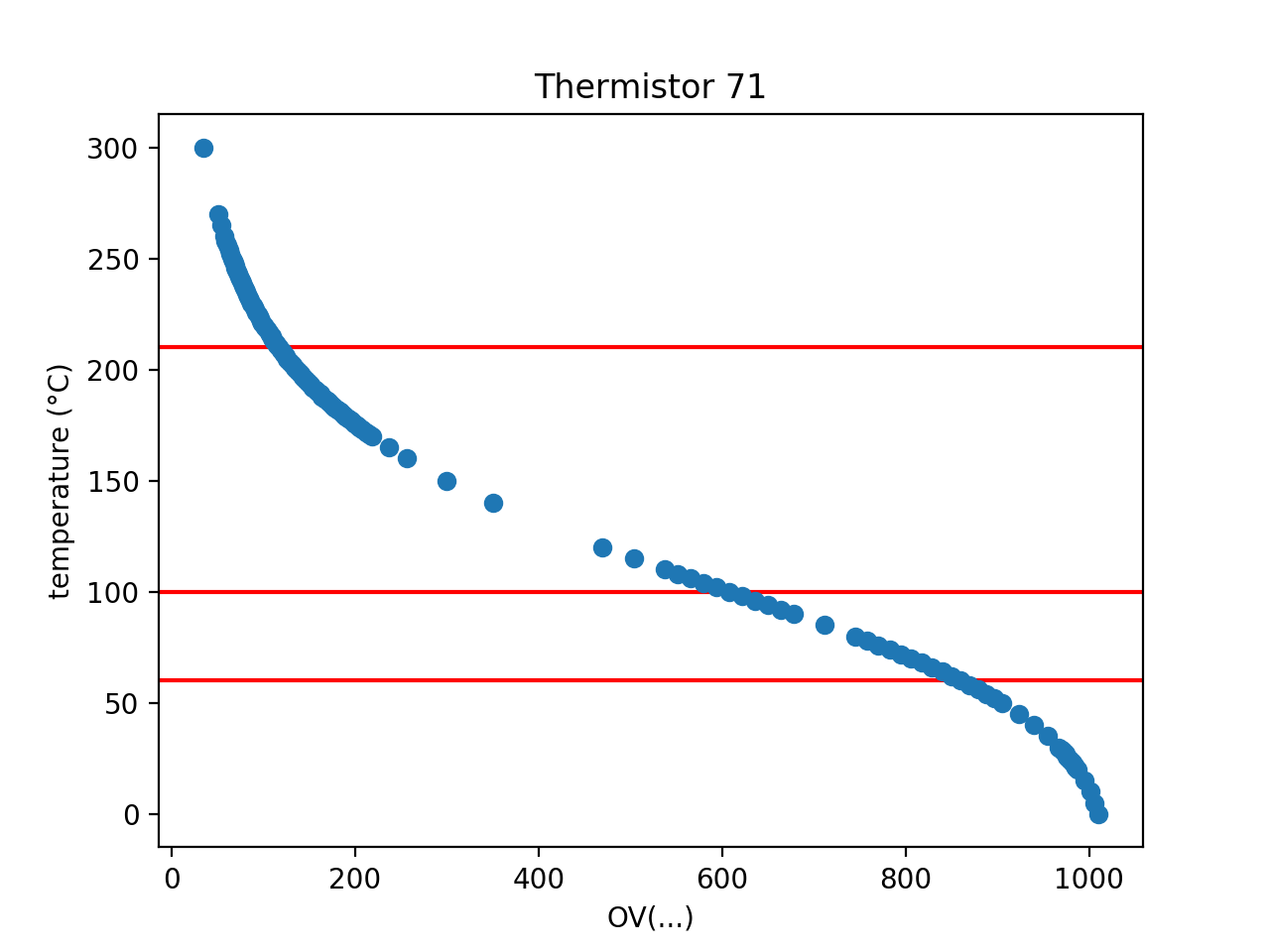
I've added red lines at 60°C, 100°C, and 210°C since that seems to be where the points are clustered. The cluster around 100°C could probably be removed with no ill effect.

Zooming in a bit, I can see what you mean by stepping. This table could stand to lose a few points.

(I still think adding the subtraction is an easy win: analog reads take tens of microseconds, plus another 5 or so to do the conversion. Adding a subtraction to the conversion will add half a microsecond, in the worst case.)

[AnHardt]

analog reads take tens of microseconds

We know about that. For that we don't wait for it. We start the conversion in one interrupt and pick up the result in the next (1ms later). Then, on the next interrupt, we start for the next temperature - ...
When we have enough samples per sensor (usually 16) we look up the value in the table (about 5 times /second/sensor).

The change to enable Marlin to use longer tables seems to be ok to me!

That does not make table 17 better. (For me 13 is an example for a better table)

[agrif]

I would be happy to dig into this problem this week, and come up with two PRs that can be merged at leisure:

• Resampling table 17 to be less terrible
• Fixing the overflow error in table lookups to allow up to 256 entries

I'm in a good position to test both of them. I've already been running the overflow fix for a few days now.

[berkus]

@agrif this overflow check was added only because some people insisted it should be there. Just disable that static assert and it will compile fine!

[agrif]

Removing the check does mean it compiles fine, but this line in temperature.cpp overflows on the long table, and so looking up a temperature loops forever.

[berkus]

@agrif this is totally fine, quoting from the discussion:

thinkyhead on May 29  • 
Seems to be completely safe from overflowing now.

[agrif]

While writing up and testing a PR to fix the overflow, I discovered something embarrassing. The code at temperature.cpp:928 does not overflow at all. It works fine, identically to the proposed fix, for all possible values of l and r.

This is integer promotion at work. Basically in C/C++, the arguments to math operators can't be smaller than int, and are boosted up if they're smaller. As a feature of the C/C++ standards, I think we can rely on it not overflowing on any board.

Test it out yourself with this simple arduino program.

[crzcrz]

I would not expect this to be happening on an 8-bit system though. Isn't it supposed to promote to the native word size?

[agrif]

By the spec, it promotes to int, which is 16-bit on ATmegas. It was surprising to me, too. I have no idea what this compiles to... it could be a full 16-bit addition and then shift, or it could just be an 8-bit addition with a shift-carry.

It was also sort of amazing that so many people (including me) have discussed this bug and nobody bothered to see if it even exists until now.

[crzcrz]

I think there's some evidence that compilers may not necessarily perform integer promotion on 8-bit CPUs. Look at example 4 here: https://electronics.stackexchange.com/a/328001

At the very least we should look at the actual assembly code, generated with Arduino IDE, as well as with GCC in PlatformIO. And even if we see extra instructions to take care of the carry flag after performing addition I would still consider this unsafe, for it may change in the next release of the compiler or with different optimisations enabled.

[crzcrz]

I looked at the disassembly of analog2temp and found the following:

add r20, r27
adc r21, r1
asr r21
ror r20

That corresponds to m = (l + r) >> 1; and also shows that there's promotion to 16 bits taking place at the cost of one additional register and two additional instructions.

I then changed the middle element computation to m = l + ((r - l) >> 1) and looked at the disassembly again:

sub r24, r22
sbc r25, r23
asr r25
ror r24
add r24, r26

That's clearly worse, and the promotion is still taking place.

So... Let's try to force it to do what we want by explicitly casting each sub-expression to 8 bits.

m = l + (uint8_t)(((uint8_t)(r - l) >> 1U));

And the assembly:

sub r24, r25
lsr r24
add r24, r25

Voila! Less instructions, less registers, and no overflow.

@thinkyhead What do you think?

[agrif]

Example 4 in the link you provided is doing exactly the same optimization that your casting does, by forcing the compiler to use 8-bit inputs to each operand and store it as 8-bit outputs. It will still promote the ints, but at the end of it all it's smart enough to know that promoting, adding, and immediately downcasting is the same as just adding as 8-bit.

I wouldn't worry too much about compilers that currently follow the spec not following it in the future. As weird as it is, promotion is standard C and C++.

The three-instruction solution is nice, though, and degrades well even if the compiler doesn't optimize at all. But I wish we could write some C that would compile just to add / ror.

Edit: another possible solution suggested by a friend: add a static assertion to check that the compiler will promote the ints, and keep the original code. Saving 40 cycles per sensor per second is neat, but not really going to have any impact.

[github-actions[bot]]

This issue has been automatically locked since there has not been any recent activity after it was closed. Please open a new issue for related bugs.