Jax: Best practice to handle division by zero in auto-differentiation

[gnool]

What is the best practice to handle functions that involve division by zero? Consider f(x) = sin(x) / x. If we define the function as follows and try to get gradient at x=0, JAX (or most likely any auto-diff package) returns nan.

def func(x):  
    return jnp.sin(x) / x

But if we define it as follows, it returns 0 (which is correct).

def func(x):
    x = x + jnp.finfo(jnp.float64).eps
    return jnp.sin(x) / x

I guess this is not so much related to JAX but more to auto-differentiation technique in general.

[jakevdp]

Automatic differentiation around limiting values is a bit tricky; there is a really detailed and useful discussion of the issue in this thread: https://github.com/google/jax/issues/1052#issuecomment-514083352

Briefly, what you need to do is rearrange your function definition so that the automatic differentiation machinery doesn't encounter NaNs.

In your case, the first thing you need is a way to ensure that func(x) evaluates to something other than NaN at x = 0.0. You can do this in a jittable way using, for example, jnp.where:

def func(x):  
    return jnp.where(x == 0, 1.0, jnp.sin(x) / x)

You'll find that func(0.0) now returns the correct result, but grad(func)(0.0) still returns NaN. To get around that, you can employ the double-where trick mentioned in thread linked above. The result would look something like this:

def func(x):
  y = jnp.where(x == 0.0, 1.0, x)
  return jnp.where(x == 0.0, 1.0, jnp.sin(y) / y)

With this definition, both func(0.0) and grad(func)(0.0) return the expected result.

[gnool]

Thanks @jakevdp for the explanation.

In the first version, what triggers nan/inf during the calculation of gradient? I had imagined that when we evaluate the gradient at x=0, we would be looking at the branch where f(x) = 1.0, and thus its derivative is 0 since its a constant. I'm sure there must be more sophisticated (i.e. correct) ways of handling these piece-wise functions at the boundaries between pieces, but beyond that I have no clue what triggers the behavior above.

To take things a bit further, would the second version of func above work for, say, grad(grad(func))(0.0)?

[jakevdp]

In the first version, what triggers nan/inf during the calculation of gradient?

The discussion at https://github.com/google/jax/issues/1052 has a detailed explanation of this, but it's essentially because the unused gradient is multiplied by zero, and 0.0 * nan = nan

To take things a bit further, would the second version of func above work for, say, grad(grad(func))(0.0)?

Yes, it should work for all gradients at this point, because the NaNs have been taken out of the picture entirely.

[gnool]

@jakevdp Thanks, will read more about the comment.

Strangely, I'm getting 0 as output at x = 0 for the second-order derivative of the function above, which seems to be wrong. If I'm doing it correctly with manual derivation, the answer should be -1/3. Any idea what went wrong?

[jakevdp]

Hmm, that is strange. It turns out to be the case for the built-in sinc function as well:

import matplotlib.pyplot as plt
import jax.numpy as jnp
from jax import grad, vmap

x = jnp.linspace(-5, 5, 101)
y = vmap(grad(grad(jnp.sinc)))(x)

plt.plot(x, y)

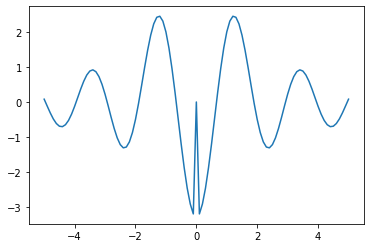
Something in the autodiff approach is not doing the right thing at x=0, and I'm not entirely sure what's going on.

[jakevdp]

So I dug into this a bit... it turns out the issue is that we replaced the x=0 value with something that has the wrong taylor expansion at x=0. We can make the 2nd-order gradient work by replacing it with something like this:

def func(x):
  y = jnp.where(x == 0.0, 1.0, x)
  return jnp.where(x == 0.0, - x ** 2 / 6.0, jnp.sin(y) / y)

But then, of course, this has the wrong 4th degree taylor expansion, so the fourth derivative will be wrong.

The mechanism that JAX provides for situations like this is the custom JVP rule, where we would treat jnp.sinc(x) as a single unit, with n-th derivatives explicitly defined. I don't know if there's any other way to allow auto-differentiation to naturally handle these sorts of cases correctly.

These kinds of pathologies around discontinuities in auto-differentiation have been studied; a useful reference is https://arxiv.org/abs/1911.04523

[mattjj]

Some commentary on #5077.

[gnool]

For a more complicated function (in my case here a batched Rodrigues function), could I get some advice on how to use the tricks above to rewrite it into a form that's differentiable up to any order N?

The function I'm using is as follows. The input r is (N, 1, 3) and output is (N, 3, 3) where the

def rodrigues(r):
    theta = jnp.linalg.norm(r, axis=(1, 2), keepdims=True)
    r_hat = r / theta
    cos = jnp.cos(theta)
    z_stick = jnp.zeros(theta.shape[0])
    m = jnp.dstack([
        z_stick, -r_hat[:, 0, 2], r_hat[:, 0, 1],
        r_hat[:, 0, 2], z_stick, -r_hat[:, 0, 0],
        -r_hat[:, 0, 1], r_hat[:, 0, 0], z_stick]
    ).reshape([-1, 3, 3])
    # create stacked 3x3 identity matrices
    i_cube = jnp.tile(jnp.eye(3),(r.shape[0],1,1))
    A = jnp.transpose(r_hat, axes=[0, 2, 1])
    B = r_hat
    dot = jnp.einsum("ink, ikm->inm", A, B)
    R = cos * i_cube + (1 - cos) * dot + jnp.sin(theta) * m
    return R

Here, the main division-by-zero issue occurs when a zero vector leads to theta=0.

[jakevdp]

So in this case, there’s no limit involved, and the gradient of r/theta for theta->0 diverges. It’s not clear to me that there’s any way around that.

[gnool]

I agree, that's the point that inf is triggered. Actually this function has a well-defined value (and its Jacobian too) when r has all zero elements. In fact OpenCV's implementation of this function and its Jacobian (as seen here) is manually handling the case where the norm is zero by returning a pre-defined matrix.