Jax: Discrepancy with autograd results

[madvn]

With the following code, I get different results with autograd(correct) vs jax(wrong)

    import autograd.numpy as np
    from autograd import grad

    import matplotlib
    matplotlib.use("TkAgg")
    import matplotlib.pyplot as plt

    def tanh(x):
        y = np.exp(-2. * x)
        return (1. - y) / (1. + y)

    ixs = np.linspace(-7,7,200)
    plt.plot(ixs, tanh(ixs), label="function")

    d1f = grad(tanh)
    plt.plot(ixs, [d1f(ix) for ix in ixs], label="deriv_1")

    d2f = grad(grad(tanh))
    plt.plot(ixs, [d2f(ix) for ix in ixs], label="deriv_2")

    d3f = grad(grad(grad(tanh)))
    plt.plot(ixs, [d3f(ix) for ix in ixs], label="deriv_3")

    d4f = grad(grad(grad(grad(tanh))))
    plt.plot(ixs, [d4f(ix) for ix in ixs], label="deriv_4")

    plt.legend()
    plt.show()

With autograd I get:

Changing the import statements to

    import jax.numpy as np
    from jax import grad

gives

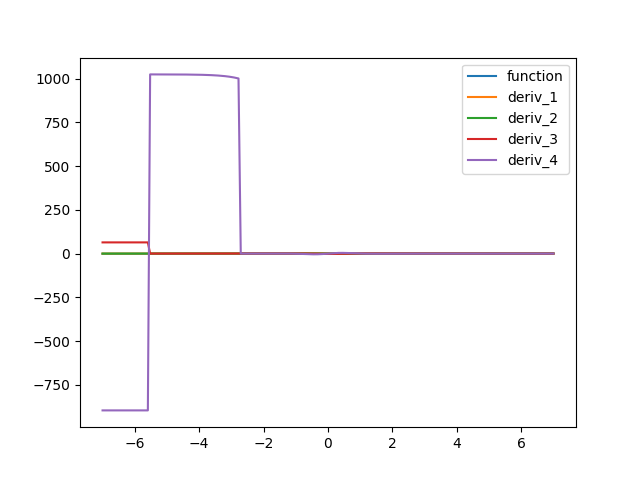
Am I missing something? Please clarify.

[mattjj]

Looks like some numerical instability... let's figure this out! Two ideas spring to mind: (1) maybe one of our differentiation rules is written in an unstable way, (2) numpy+autograd is using f64 by default, whereas jax uses f32 by default.

By the way, your code will be much faster if you do this:

from jax import grad, vmap

ixs = np.linspace(-7,7,200)
plt.plot(ixs, tanh(ixs), label="function")

d1f = grad(tanh)
plt.plot(ixs, vmap(d1f)(ixs), label="deriv_1")

d2f = grad(grad(tanh))
plt.plot(ixs, vmap(d2f)(ixs), label="deriv_2")

d3f = grad(grad(grad(tanh)))
plt.plot(ixs, vmap(d3f)(ixs), label="deriv_3")

d4f = grad(grad(grad(grad(tanh))))
plt.plot(ixs, vmap(d4f)(ixs), label="deriv_4")

That seems to change the numerical behavior a bit too (for the better).

[hawkinsp]

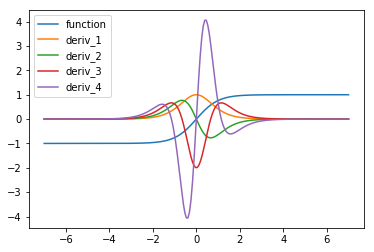
In float64 mode it seems to match autograd. I ran the following in a Google Colab (after first running !pip install jax jaxlib):

import jax.numpy as np
from jax import grad, vmap
from jax.config import config
config.update("jax_enable_x64", True)

import matplotlib
import matplotlib.pyplot as plt

def tanh(x):
  y = np.exp(-2. * x)
  return (1. - y) / (1. + y)


ixs = np.linspace(-7,7,200)
plt.plot(ixs, tanh(ixs), label="function")

d1f = grad(tanh)
plt.plot(ixs, vmap(d1f)(ixs), label="deriv_1")

d2f = grad(grad(tanh))
plt.plot(ixs, vmap(d2f)(ixs), label="deriv_2")

d3f = grad(grad(grad(tanh)))
plt.plot(ixs, vmap(d3f)(ixs), label="deriv_3")

d4f = grad(grad(grad(grad(tanh))))
plt.plot(ixs, vmap(d4f)(ixs), label="deriv_4")
plt.legend()
plt.savefig("autograd_derivs.png")

and get:

[mattjj]

I also verified that Autograd does the same on f32 (and there isn't really much room for a numerically unstable derivative rule here anyway):

import autograd.numpy as np
from autograd import elementwise_grad as egrad

import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as plt

def tanh(x):
    y = np.exp(-2. * x)
    return (1. - y) / (1. + y)

ixs = np.linspace(-7, 7, 200).astype("float32")
plt.plot(ixs, tanh(ixs), label="function")

d1f = egrad(tanh)
plt.plot(ixs, d1f(ixs), label="deriv_1")

d2f = egrad(egrad(tanh))
plt.plot(ixs, d2f(ixs), label="deriv_2")

d3f = egrad(egrad(egrad(tanh)))
plt.plot(ixs, d3f(ixs), label="deriv_3")

d4f = egrad(egrad(egrad(egrad(tanh))))
plt.plot(ixs, d4f(ixs), label="deriv_4")

plt.legend()
plt.show()

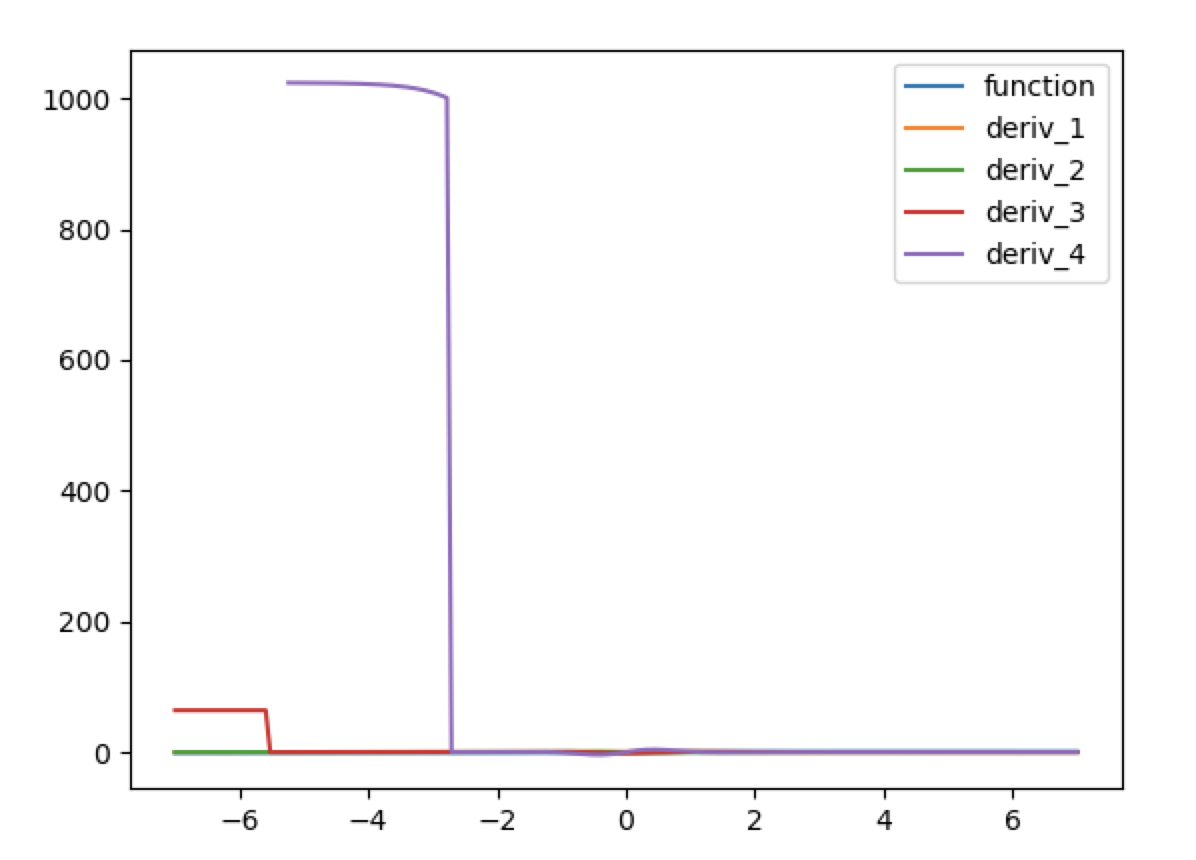
(By the way, elementwise_grad is the canonical way to write this kind of thing in Autograd. It only works if the function being differentiated acts elementwise, otherwise it silently gives the wrong answer, unlike vmap.)

I think we've sorted this issue out: it's just about f64 vs f32. Though Autograd and JAX have different defaults, they behave the same in the two settings.