Jax: Time-efficient higher-order forward mode?

[duvenaud]

Have you guys given any thought to how to efficiently compute higher-order derivatives of scalar-input functions? I have a use for 4th- and 5th-order derivatives of a scalar-input, vector-output function, namely, regularizing ODEs to be easy to solve.

I'm not sure, but I think that in principle, the Nth-order derivative of a scalar-input function can be computed for about only N times the cost of evaluating the original function, if intermediate values are cached. We think we have a partial solution using https://github.com/JuliaDiff/TaylorSeries.jl, but I'd rather do it in JAX.

The following toy example takes time exponential in the order of the derivative:

from jax import jvp
import jax.numpy as np

def fwd_deriv(f):
  def df(x):
    return jvp(f, (x,), (1.0,))[1]
  return df

def f(t):
    return 0.3 * np.sin(t) * t**10

g = f
for i in range(10):
    g = fwd_deriv(g)
    print(g(1.1))

Is there a simple way to set things up with jvps and vjps to be more time-efficient, or do you think it would require a different type of autodiff entirely?

[mattjj]

Great question.

One potential quick fix is that if you use @jit then XLA's common-subexpression elimination (CSE) might do some of this for you. But exponentially blowing up the computation we hand to XLA isn't a good idea even if XLA can CSE it back down.

Here's an adapted version of your script that shows the blowup:

from __future__ import print_function

from jax import jvp
import jax.numpy as np
from jax import make_jaxpr

def fwd_deriv(f):
  def df(x):
    return jvp(f, (x,), (1.0,))[1]
  return df

def f(t):
    return 0.3 * np.sin(t) * t**10

g = f
for i in range(5):
    g = fwd_deriv(g)
    print(g(1.1))
    jaxpr = make_jaxpr(g)(1.1)
    # print(jaxpr)  # uncomment to show the blowup
    print(len(jaxpr.eqns))

Here are the first two jaxprs:

6.657216
{ lambda b o n g k m e ;  ; a.
  let c = cos a
      d = mul b c
      f = mul d e
      h = pow a g
      i = mul f h
      j = sin a
      l = mul j k
      p = pow a o
      q = mul n p
      r = safe_mul m q
      s = mul l r
      t = add_any i s
  in t }

57.3042
{ lambda bs j bp s m br bc bo be bf c p bq bg h t b bm r z ;  ; a.
  let d = sin a
      e = mul c d
      f = neg e
      g = mul b f
      i = mul g h
      k = pow a j
      l = mul i k
      n = cos a
      o = mul m n
      q = mul o p
      u = pow a t
      v = mul s u
      w = safe_mul r v
      x = mul q w
      y = add_any l x
      ba = cos a
      bb = mul z ba
      bd = mul bb bc
      bh = pow a bg
      bi = mul bf bh
      bj = safe_mul be bi
      bk = mul bd bj
      bl = sin a
      bn = mul bl bm
      bt = pow a bs
      bu = mul br bt
      bv = safe_mul bq bu
      bw = mul bp bv
      bx = safe_mul bo bw
      by = mul bn bx
      bz = add_any bk by
      ca = add_any y bz
  in ca }

I thought reusing intermediate values was also an original motivation of our recursively-defined derivatives code, i.e.

def pushfwd(f, x, vs):
  if vs:
    v, vs = vs[0], vs[1:]
    return jvp(lambda z: pushfwd(f, z, vs), (x,), (v,))[1]
  else:
    return f(x)

but it doesn't seem to help here.

[mattjj]

I forgot to add: I don't know the answer, but let's try to figure it out!

[mattjj]

Some more info on the nature of the blowup, following on from that last script:

from collections import Counter

counts = Counter(eqn.primitive.name for eqn in jaxpr.eqns)
print(counts.most_common())

[('mul', 224),
 ('safe_mul', 80),
 ('pow', 32),
 ('neg', 32),
 ('add_any', 31),
 ('cos', 16),
 ('sin', 16)]

[mattjj]

Now with more plotting!

from jax import jvp, make_jaxpr
import jax.numpy as np
from collections import Counter, defaultdict
import matplotlib.pyplot as plt

def fwd_deriv(f):
  def df(x):
    return jvp(f, (x,), (1.0,))[1]
  return df

def f(t):
    return 0.3 * np.sin(t) * t**10

dmax = 8

g = f
primitive_counts = defaultdict(list)
for i in range(dmax):
    g = fwd_deriv(g)
    print(g(1.1))
    jaxpr = make_jaxpr(g)(1.1)
    c = Counter(eqn.primitive.name for eqn in jaxpr.eqns)
    for name, count in c.most_common():
      primitive_counts[name].append(count)

fig, ax = plt.subplots()
for name, counts in primitive_counts.items():
  counts = [0] * (dmax - len(counts)) + counts
  ax.plot(counts, label=name)
ax.legend()

So I suspect that everything may be exponential, but some things are more exponential than others.

[mattjj]

We discussed this a bit in our chat. We think the answer is to add a CSE pass that happens after every level of differentiation. But we might also need some other simplifications, like collecting terms x + x + x = 3x.

CSE is easy enough to add. We'll try it out and report back!

[duvenaud]

Wow, thanks for looking into this so quickly!

[mattjj]

In fb22275 over on the jaxch-cse branch I just pushed, @dougalm and @axch and I sketched out a really basic CSE based on simply memoizing Primitive.bind.

Currently the notion of equality is too specific and so we're not getting enough cache hits. In particular, while we've crushed sin/cos/neg down to be constant (instead of exponential), we're generating too many muls and adds:

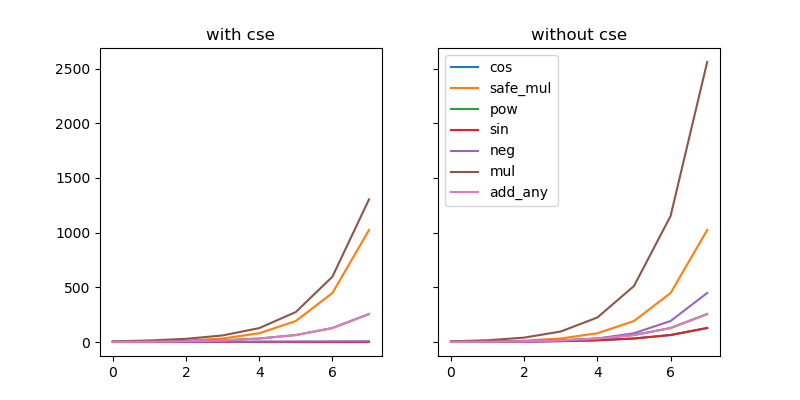
from collections import Counter, defaultdict

import matplotlib.pyplot as plt

import jax.numpy as np
from jax import jvp, make_jaxpr
from jax import core

def fwd_deriv(f):
  def df(x):
    return jvp(f, (x,), (1.0,))[1]
  return df

def f(t):
  return 0.3 * np.sin(t) * t**10

dmax = 8
fig, [ax1, ax2] = plt.subplots(1, 2, sharey=True, sharex=True, figsize=(8, 4))

for enable_cse, ax in [(True, ax1), (False, ax2)]:
  core.enable_cse = enable_cse

  primitive_counts = defaultdict(list)
  g = f
  for i in range(dmax):
    g = fwd_deriv(g)
    print(g(1.1))
    jaxpr = make_jaxpr(g)(1.1)
    print(len(jaxpr.eqns))
    c = Counter(eqn.primitive.name for eqn in jaxpr.eqns)
    for name, count in c.most_common():
      primitive_counts[name].append(count)

  for name, counts in primitive_counts.items():
    counts = [0] * (dmax - len(counts)) + counts
    ax.plot(counts, label=name)
  ax.set_title("{} cse".format("with" if enable_cse else "without"))

ax.legend()

fig.savefig('hi.png')

(There could be an issue in how I'm doing this count: forming a jaxpr could itself be foiling this simple CSE, and so I should switch to counting hits/misses directly on the cache without using make_jaxpr at all.)

There may be simple things we can do to improve the value equality testing. Or we might need to add invariance to commutation and maybe even association (which we know how to do).

The good news is that all the tests pass. It's easy to make memoization sound!

We're split on whether we should just push forward this simple "memoize bind" model of CSE, or whether we should add an explicit tracer/final-style transformation for it. Not sure yet what the tradeoffs are. The latter involves more boilerplate, more runtime overhead, and doesn't automatically cover the whole system, but may be easier to reason about and offer more control.

By the way, an alternative to doing CSE is "Taylor series propagation", which we could also implement in JAX. That would basically mean making a new Tracer that is kind of like JVPTracer, except instead of modeling values of the form a + b * eps, the tracer payload would model values of the form a + b * eps + c * eps^2, or more generally any order. So we'd have a TaylorSeriesTracer(order=N), and JVPTracer = TaylorSeriesTracer(order=1). The fundamental issue that would tackle is (borrowing from an @axch explanation) that currently jvp(jvp(f)) evaluates f on ((a + a1 * eps) + (a1 + a11 * eps) * eps), meaning we have 4 terms where really we should have 3 because the two instances of a1 can be collected. That means jvp**5 takes 32 terms where we only really need 6.

But ultimately implementing that is just going to be a limited form of CSE: basically when we evaluate each primitive we'll do some CSE to collect those 32 terms down to 6 (for the case of jvp**5). If we're going to implement CSE anyway, we should just do it properly on a way that extends to everything in the system. Moreover, just implementing a TaylorSeriesTracer leaves open the hardest part: how you merge together lower-order TaylorSeriesTracers that arose from separately kicked-off jvp transformations.

So to summarize, as far as I currently know, Taylor series propagation is only useful if your system can't implement a good CSE that can be interleaved with AD passes. And it opens up issues that may be harder to solve than general CSE. We think JAX can do better!

[mattjj]

(I'm juggling some SPMD stuff right now, and @dougalm is working on differentiable scan, so we haven't spent much time on this so far, but we'll come back to it as we can!)

[mattjj]

Not directly related, but check out the jarrett-jvps branch jarrett-jvps-2 branch where we just sketched out an implementation of this optimization.

Here's the punchline:

from jax import jarrett, vjp, make_jaxpr
import jax.numpy as np

def f(x):
  return np.sin(np.sin(np.sin(x)))
f2 = jarrett(f)

print f(3)
print f2(3)
print

_, f_vjp = vjp(f, 3.)
_, f2_vjp = vjp(f2, 3.)
print f_vjp(1.)
print f2_vjp(1.)
print

print make_jaxpr(f_vjp)(1.)
print make_jaxpr(f2_vjp)(1.)

0.14018878
0.14018878

(array(-0.9704719, dtype=float32),)
(array(-0.9704719, dtype=float32),)

{ lambda e i g ;  ; a.
  let b = pack * a
      (c d) = id b
      f = mul d e
      h = mul f g
      j = mul h i
      k = pack j
      (l) = id k
      m = pack l
  in m }

{ lambda e ;  ; a.
  let b = pack * a
      (c d) = id b
      f = mul d e
      g = pack f
      (h) = id g
      i = pack h
  in i }

For a chain of elementwise unary ops, we only have to store one linearization point, regardless of the depth of the chain. That means if you have a network with gelu activations, as in

def gelu(x):
    return 0.5*x*(1+np.tanh(np.sqrt(2/np.pi)*(x+0.044715 * lax.pow(x, 3))))

in reverse-mode you only store one activations-sized constant per layer (as opposed to one per nonlinear op in the activation function).

EDIT: though gelu has binary operations too, and so far that PR only does things to unary operations.

EDIT 2: Actually the version in jarrett-jvps-2 is much better! It handles arbitrary arity in many fewer lines of code, with user control of the tradeoffs. I updated the above text. See also #525.

[mattjj]

Some progress over here: https://github.com/google/jax/compare/cse

EDIT: updated numbers

from collections import Counter

def deriv(f):
  return lambda x: jvp(f, (x,), (1.,))[1]


def f(x):
  return 0.3 * np.sin(x) * x ** 10

g = f
for i in range(8):
  jaxpr = make_jaxpr(g)(3.)
  print(g(3.), Counter(eqn.primitive for eqn in jaxpr.eqns).most_common())

  g = deriv(g)

Without CSE (i.e. on master):

(array(2499.8987, dtype=float32), [(mul, 2), (sin, 1), (pow, 1)])
(array(-9204.425, dtype=float32), [(mul, 6), (pow, 2), (add_any, 1), (cos, 1), (safe_mul, 1), (sin, 1)])
(array(-94417.05, dtype=float32), [(mul, 16), (safe_mul, 4), (pow, 4), (add_any, 3), (cos, 2), (sin, 2), (neg, 1)])
(array(-466920.22, dtype=float32), [(mul, 40), (safe_mul, 12), (pow, 8), (add_any, 7), (cos, 4), (neg, 4), (sin, 4)])
(array(-1628770.6, dtype=float32), [(mul, 96), (safe_mul, 32), (pow, 16), (add_any, 15), (neg, 12), (cos, 8), (sin, 8)])
(array(-4033757.8, dtype=float32), [(mul, 224), (safe_mul, 80), (pow, 32), (neg, 32), (add_any, 31), (cos, 16), (sin, 16)])
(array(-5534321.5, dtype=float32), [(mul, 512), (safe_mul, 192), (neg, 80), (pow, 64), (add_any, 63), (cos, 32), (sin, 32)])
(array(5498716., dtype=float32), [(mul, 1152), (safe_mul, 448), (neg, 192), (pow, 128), (add_any, 127), (cos, 64), (sin, 64)])

With CSE (i.e. on that branch):

(array(2499.8987, dtype=float32), [(mul, 2), (sin, 1), (pow, 1)])
(array(-9204.425, dtype=float32), [(mul, 6), (pow, 2), (add_any, 1), (cos, 1), (safe_mul, 1), (sin, 1)])
(array(-94417.05, dtype=float32), [(mul, 14), (safe_mul, 4), (pow, 4), (add_any, 3), (cos, 1), (neg, 1), (sin, 1)])
(array(-466920.22, dtype=float32), [(mul, 29), (safe_mul, 12), (pow, 8), (add_any, 7), (neg, 2), (cos, 1), (sin, 1)])
(array(-1628770.6, dtype=float32), [(mul, 60), (safe_mul, 32), (pow, 16), (add_any, 15), (neg, 3), (cos, 1), (sin, 1)])
(array(-4033757.8, dtype=float32), [(mul, 127), (safe_mul, 80), (pow, 32), (add_any, 31), (neg, 4), (cos, 1), (sin, 1)])
(array(-5534321.5, dtype=float32), [(mul, 274), (safe_mul, 192), (pow, 64), (add_any, 63), (neg, 5), (cos, 1), (sin, 1)])
(array(5498716., dtype=float32), [(mul, 597), (safe_mul, 448), (pow, 128), (add_any, 127), (neg, 6), (cos, 1), (sin, 1)])

Might be doing something dumb with that pack/unpack stuff. Also I should add this is only lightly tested so might not actually be correct yet :) I was using both primal and tangent outputs of jvp instead, i.e. my fwd_deriv function wasn't doing what we wanted.

That branch is using an explicit cse JAX-style transformation, rather than memoizing all bind calls. Still exploring which strategy is better. But this one is the first that let us make it robust to associativity and commutativity of addition (and, currently, multiplication as well).

[mattjj]

I've been saying "CSE" when I mean "CSE with algebraic simplifications". It's actually the simplifications that are the most important. The implementation so far handles commutativity and associativity of add and mul separately, but the most important thing for higher-order autodiff is handling them together with distributivity (i.e. a ring). Working on that with @dougalm now! We might end up separating a cse from an algsimp, not sure.

[mattjj]

By the way, this works on the cse branch right now, but I haven't had time to touch it since the weekend:

def f(x):
  return 0.3 * np.sin(x) * x ** 10

def deriv(f, x, t):
  return jvp(f, (x,), (t,))[1]

def poly(t):
  df = lambda x: deriv(f, x, t)
  ddf = lambda x: deriv(df, x, t)
  dddf = lambda x: deriv(ddf, x, t)
  ddddf = lambda x: deriv(dddf, x, t)
  return ddddf(2.)

print make_jaxpr(poly)(1.)
print make_jaxpr(polysimp.polysimp(lu.wrap_init(poly)).call_wrapped)((1.,))

{ lambda i hf gk cw dj fs ev di x eb cs hg bl r ca bc gs cz ge dz gj ex du b el be er gi fj gg cl fd ei k hh cc hj fw fz ey m bh gw bv ee hi gx cf gu gy cy cj fy fh bo de dk cm ff t fi ek bn dg ;  ; a.
  let c = mul a b
      d = neg c
      e = mul a d
      f = mul a e
      g = neg f
      h = mul a g
      j = mul h i
      l = mul j k
      n = mul a m
      o = mul a n
      p = neg o
      q = mul a p
      s = mul q r
      u = safe_mul a t
      v = mul s u
      w = add_any l v
      y = mul a x
      z = mul a y
      ba = neg z
      bb = mul a ba
      bd = mul bb bc
      bf = safe_mul a be
      bg = mul bd bf
      bi = mul a bh
      bj = neg bi
      bk = mul a bj
      bm = mul bk bl
      bp = safe_mul a bo
      bq = mul bn bp
      br = safe_mul a bq
      bs = mul bm br
      bt = add_any bg bs
      bu = add_any w bt
      bw = mul a bv
      bx = mul a bw
      by = neg bx
      bz = mul a by
      cb = mul bz ca
      cd = safe_mul a cc
      ce = mul cb cd
      cg = mul a cf
      ch = neg cg
      ci = mul a ch
      ck = mul ci cj
      cn = safe_mul a cm
      co = mul cl cn
      cp = safe_mul a co
      cq = mul ck cp
      cr = add_any ce cq
      ct = mul a cs
      cu = neg ct
      cv = mul a cu
      cx = mul cv cw
      da = safe_mul a cz
      db = mul cy da
      dc = safe_mul a db
      dd = mul cx dc
      df = mul a de
      dh = mul df dg
      dl = safe_mul a dk
      dm = mul dj dl
      dn = safe_mul a dm
      do = mul di dn
      dp = safe_mul a do
      dq = mul dh dp
      dr = add_any dd dq
      ds = add_any cr dr
      dt = add_any bu ds
      dv = mul a du
      dw = mul a dv
      dx = neg dw
      dy = mul a dx
      ea = mul dy dz
      ec = safe_mul a eb
      ed = mul ea ec
      ef = mul a ee
      eg = neg ef
      eh = mul a eg
      ej = mul eh ei
      em = safe_mul a el
      en = mul ek em
      eo = safe_mul a en
      ep = mul ej eo
      eq = add_any ed ep
      es = mul a er
      et = neg es
      eu = mul a et
      ew = mul eu ev
      ez = safe_mul a ey
      fa = mul ex ez
      fb = safe_mul a fa
      fc = mul ew fb
      fe = mul a fd
      fg = mul fe ff
      fk = safe_mul a fj
      fl = mul fi fk
      fm = safe_mul a fl
      fn = mul fh fm
      fo = safe_mul a fn
      fp = mul fg fo
      fq = add_any fc fp
      fr = add_any eq fq
      ft = mul a fs
      fu = neg ft
      fv = mul a fu
      fx = mul fv fw
      ga = safe_mul a fz
      gb = mul fy ga
      gc = safe_mul a gb
      gd = mul fx gc
      gf = mul a ge
      gh = mul gf gg
      gl = safe_mul a gk
      gm = mul gj gl
      gn = safe_mul a gm
      go = mul gi gn
      gp = safe_mul a go
      gq = mul gh gp
      gr = add_any gd gq
      gt = mul a gs
      gv = mul gt gu
      gz = safe_mul a gy
      ha = mul gx gz
      hb = safe_mul a ha
      hc = mul gw hb
      hd = safe_mul a hc
      he = mul gv hd
      hk = safe_mul a hj
      hl = mul hi hk
      hm = safe_mul a hl
      hn = mul hh hm
      ho = safe_mul a hn
      hp = mul hg ho
      hq = safe_mul a hp
      hr = mul hf hq
      hs = add_any he hr
      ht = add_any gr hs
      hu = add_any fr ht
      hv = add_any dt hu
  in hv }

{ lambda b ;  ; a.
  let (c) = id a
      d = mul b c
      e = mul d c
      f = mul e c
      g = mul f c
  in g }

We need to do that polynomial simplification on the tangents (that buys us everything that Taylor propagation does), plus it's probably a good idea to do CSE on the primals (to solve the "cosine problem").

Will update more when I can get back to this :)

[duvenaud]

Whoa, that's encouraging! Barak Pearlmutter would be impressed. I'm gaining hope that this might be ready in time for thus year's NIPS push.

[mattjj]

Remind me, when's the NIPS push? I think we can make it happen, though since us JAX folx are juggling a lot of competing priorities, it's good to have a sense for the urgency of things we want to achieve. (For example, I haven't picked this back up since my last comment.)

[duvenaud]

The submission deadline is May 23rd, so I'm already a little pessimistic, but if we don't have custom VJPs (to let us finish porting over neural ODEs) then it's a bit of a moot point anyways. However, I'm encouraged by the jax_taylor.py demo!

[proteneer]

Not to hi-jack the thread, but I have a very similar use case except its reversed: vector inputs and scalar output. So presumably an efficient way of doing jacfwd for your case can be somewhat easily ported over to an efficient jacrev for my use-case.

Just adding a +1 to show that I'm also interested in a solution to this (at least up to second order).

[mattjj]

Woo, we fixed this in #2363 ! Wow, that took some real effort :)

[jessebett]

This was definitely a bit of a rabbit hole we stumbled into!