Elasticsearch: Bug: percentiles aggregation does not behave as expected

[redlus]

Hi,

As discussed in the forums, we're seeing odd behavior when using the percentiles aggregations, the exact opposite of what is written in the documentation.

Elasticsearch version:
6.3.2

Plugins installed:
ingest-geoip
ingest-user-agent
mapper-murmur3
mapper-size
repository-azure
repository-gcs
repository-s3

JVM version:
openjdk 10.0.2 2018-07-17
OpenJDK Runtime Environment 18.3 (build 10.0.2+13)
OpenJDK 64-Bit Server VM 18.3 (build 10.0.2+13, mixed mode)

OS version:
Linux 4.9.0-6-amd64 #1 SMP Debian 4.9.82-1+deb9u3 (2018-03-02) x86_64 x86_64 x86_64 GNU/Linux

Description of the problem including expected versus actual behavior:
I've been experimenting with percentile aggregations on some dataset after receiving some odd results in elasticsearch 6.3.2.

My dataset consists of 467 floating point numbers, which can be found here. Just to rule out different implementations of the analyzed values, I've ingested this dataset (each value as a single document) into two indices - one which defines the field as a float, and one which defines the field as a scaled_float with "scaling_factor": 1000. The percentiles requested are "percents": [50, 90, 95, 99, 99.99]. In both cases, the results are very similar (between float and scaled_float) and are very different from the percentiles expected (vs. Python's NumPy):

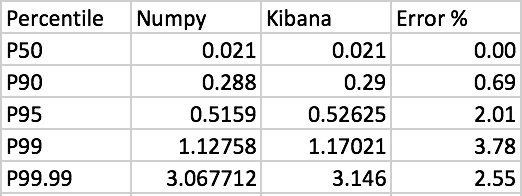
In both cases, the ingestion was into an index with a single shard and different settings of the compression parameter were tested (up to 2,000) - without affecting the end result.

As documented, I know percentiles are approximated. However, it seems that the approximation behaves exactly opposite to what is written in the documentation:

• Accuracy is proportional to q(1-q) . This means that extreme percentiles (e.g. 99%) are more accurate than less extreme percentiles, such as the median
• For small sets of values, percentiles are highly accurate (and potentially 100% accurate if the data is small enough).

My dataset is pretty small (only 467 samples), and the accuracy increases as we approach the median. How can this be explained?

Thanks.

[markharwood]

Thanks for this.

are very different from the percentiles expected (vs. Python's NumPy):

Not if you use numpy's "nearest" interpolation:

print np.percentile(a, 99.99, interpolation="nearest")
3.146

I suppose we have to be careful on which basis we're making these comparisons. Does this change your thinking?
Given this implementation is based on an established algorithm I think I'll label this as a potential documentation issue rather than an implementation issue.

[elasticmachine]

Pinging @elastic/es-analytics-geo

[polyfractal]

I haven't tested it, but I suspect this is just due to the size of the data and how it interacts with the TDigest algorithm. compression affects how many centroids are allowed before the algorithm merges centroids together. A value of n for compression allows roughly n * 20 centroids to be tracked before a merge is kicked off.

Generally, we say that more extreme percentiles are more accurate because the algorithm prefers to merge "interior" centroids and keep finer granularity at the extremes of the histogram. So as centroids are merged, you tend to lose accuracy closer to the median.

I'm guessing the small number values simply aren't using the available centroids in a manner that improves accuracy, and the "inverse" relationship you're seeing is just an artifact of how the data is laid out and due to the fact that a merge likely hasn't happened (default compression is 100, meaning potentially up to 20,000 centroids before merging which is << your data size).

[polyfractal]

Also to Mark's point, I agree that this is probably just a documentation issue regarding small sizes, and that how percentiles are interpolated matters (both externally, and how TDigest interpolates between centroids to derive the requested value)

[redlus]

@markharwood

Not if you use numpy's "nearest" interpolation:

print np.percentile(a, 99.99, interpolation="nearest")
3.146

I suppose we have to be careful on which basis we're making these comparisons. Does this change your thinking?
Given this implementation is based on an established algorithm I think I'll label this as a potential documentation issue rather than an implementation issue.

Good point. Most default implementations I know of usually utilize linear interpolation (that includes Python's NumPy, the interpolation function in MS Excel, R's quantile function etc). I believe it should be documented if elastic's algorithm behaves differently. Also, it may be a good feature request if it is possible to choose which interpolation method it will use 👍🏼

[polyfractal]

I'm not sure we can support different interpolations, because TDigest has to deal with a different environment than numpy/excel/R/etc. Those simple percentile computations benefit from having all the data, so they can choose how to interpolate between data points when the requested rank isn't represented directly.

TDigest only has access to centroids which summarize parts of the CDF, and so implicitly has to perform interpolation to approximate the requested percentile. This interpolation also varies depending on the nature of the centroids (does the centroid represent an exact data point? Is it a summary of multiple points? is this the last centroid on either extreme?)

If you're interested, the TDigest paper discusses interpolation in section "2.9. Interpolation of the cumulative distribution function" :)

[polyfractal]

Going to close this. Been thinking about how or if we want to document, and I think it's redundant since we link to the TDigest paper in the docs. I don't want to rewrite how the algo works in detail (that's why we link to the paper), and I don't think there's a sufficiently strong reason to get into the nitty-gritty details about how the algo interpolates while ignoring the rest of the algo.