Csswg-drafts: [css-easing-2] Complex easing/timing functions

[rachelnabors]

In light of the Webkit team's implementation of spring(), it's apparent we need to attend to the issue of complex timing functions sooner rather than later.

The problem

Designers often need more advanced timing functions than can be described with cubic-beziers. They are not limited to spring functions, either. A common problem is there is no effective way to export a timing graph from Adobe After Effects to a timing function that could be used with CSS or with the Web Animations API. Currently designers have to hack together individual timing functions using CSS animation keyframes, which is impossible to do by hand in all but the most trifling instances.

spring() is just a bandaid.

The solution

We need a format to write functions like spring() in, one that we can export to from software like AfterEffects and prototyping tools that have yet to be built.

I am not in a position to propose the technical specifications of this solution. But there are people who have that knowledge. I have invited them (@visiblecode) to share their proposals below.

[birtles]

There is some previous discussion of this topic, thread starting here: https://lists.w3.org/Archives/Public/public-fx/2015JulSep/0034.html

[visiblecode]

Cubic beziers aren't a bad choice for timing functions. They're very easy to evaluate (just a few additions and multiplications). Also, most animation tools use some form of cubic spline to specify animation paths, which can be converted into cubic bezier easings with good fidelity.

There are two problems with cubic-bezier() as it is currently specced, however:

1. You can't specify a spline of multiple segments
2. cubic-bezier() is abusing 2d parametric curves to specify 1d functions

The first issue can be addressed by, essentially, just adding more points to the cubic-bezier() syntax. I believe this has already been proposed in various forms.

The second issue is pretty significant, though, and deserves some unpacking. cubic-bezier() is specified as a _2d_ bezier, a 2d parametric curve. This has a lot of implications, including:

1. Without additional constraints, the resulting curve isn't guaranteed to have a singular y value for a given x and can't be used to define a mathematical function. This has been dealt with by restricting x to the range [0, 1], but that doesn't actually address the root (no pun) problem -- because a cube root is involved there are still two extra solutions in the complex plane.
2. As mentioned, implementors must solve cube roots to work backwards from x to the implicit t parameter, before they get to the normal (and much simpler/exact!) bezier calculation to evaluate the easing function.
3. Tool authors who want to do a direct conversion of cubic spline segments to cubic-bezier()s have no use at all for the extra dimension, but must clutter the output with decimal approximations of 1/3 and 2/3.

The extra dimension isn't useful and makes life harder for implementors and tool authors alike. Ideally, instead of having to specify a two-dimensional curve like cubic-bezier(0.33333, 0.4, 0.66666, 0.6), we ought to have gotten _one-dimensional_ curves, e.g. cubic-bezier(0.4, 0.6).

With one dimension, instead of having to work backwards from (normalized) time to an implicit t, the normalized time could be used directly as the input without having to solve cube roots first.

I guess if I were going to make a concrete proposal, I'd like to see syntax for specifying 1d bezier splines, in a format something like cubic-spline(c, [c,t,c,]* c) (where the cs and ts are numbers).

The first and last values are exactly like the control points in cubic-bezier(), except since we're only dealing with one dimension, the "control points" are specified by scalar values, rather than pairs of them.

Between those end "control values", you could have zero or more (control value, time, control value) triples representing intermediate knots with their adjacent control "points". The knot times (the middle value of the triples) would have to be monotonically increasing, in the range (0, 1).

As a concrete example, let's take the following complex easing:

 @keyframes example {
     from {
         some-property: 100px;
         animation-timing-function: cubic-bezier(0.33333, 0.25, 0.66666, 0.8);
     }
     50% {
         some-property: 75px;
         animation-timing-function: cubic-bezier(0.33333, 0.5, 0.66666, 0.6);
     }
     to {
         some-property: 50px;
     }
 }

Given the aforementioned cubic-spline() function, you could define the same animation more simply as:

 @keyframes example {
     from {
         some-property: 100px;
         animation-timing-function: cubic-spline(0.125, 0.4,0.5,0.75, 0.8);
     }
     to {
         some-property: 50px;
     }
 }

IMO this seems better for both export tooling and hand authoring.

One thing this proposal doesn't address are use cases where you want easings/animations with sudden jumps in them. (i.e. not C0 continuous) Having multiple intermediate CSS keyframes may still be a good answer for animations with discontinuities (rather than trying to define timing functions with discontinuities), though in order to do that there would need to be a mechanism to specify different incoming and outgoing property values for a CSS keyframe.

[visiblecode]

One of the things that bothers me about spring() specifically is that it requires finding an approximate solution to a differential equation, just like cubic-bezier() requires approximate solving of cube roots (only moreso). Browsers' approximations will vary, and there are performance/quality tradeoffs.

Using (1d) bezier splines for defining easing functions is far simpler than something like spring() computationally, and is easy to pull off with good precision. It's also relatively easy for tools to "bake" a physically-based animation (including ones much more complex than spring simulations) into a spline, which animation tools do anyway for better reproduceability and performance.

[visiblecode]

Thinking about it overnight, cubic-polybezier() might be a more accurate/less misleading name than cubic-spline(). I'll let other people bikeshed about naming though.

[visiblecode]

I'm also an idiot; those triples need to be four-tuples, there's an extra position parameter which I left out. So that example/proposal is wrong.

[visiblecode]

Adding the missing position parameter to the two control values, the syntax would be something like cubic-spline(c, [c, t, p, c,]* c). And that example becomes:

@keyframes {
    from {
        some-property: 100px;
        animation-timing-function: cubic-spline(0.125, 0.4, 0.5,0.5, 0.75, 0.8);
    }
    to {
        some-property: 50px;
    }
}

[visiblecode]

Having thought about this for a while and chatted with others, I think the minimum required features for representing complex easing functions boil down to:

• piecewise
• cubic functions
• with jump discontinuities
• of chosen directional continuity

Piecewise cubics are pretty much the common denominator for animation software, which either uses some form of piecewise cubic spline directly, or else curves which are reasonably easy to convert to piecewise cubics.

The main exception are animation tools which are doing physical simulations. Even then, some simple physical systems can be directly represented. For example, piecewise cubics are more than enough to precisely represent physically-accurate "bouncing ball" easings, since ballistic trajectories are simple parabolic arcs.

Oscillating spring (or pendulum) easings are sinusoidal and _not_ exactly representable using simple polynomials, but you can still do a good job of approximating them by gluing multiple cubic segments together. If spring() became part of the standard, it might make sense to define it in terms of an appropriate piecewise cubic approximation.

I don't know how often jump continuities are really needed in easing functions, but they're certainly required if you want to be able to define a single easing function to recreate existing complex @keyframes animations which use timing functions like step-start() or step-end(). So it seems worth including them.

[visiblecode]

It's probably worth observing that _motion_ curves (as opposed to _timing_/easing curves) in animation software are a little bit of a different story. There you're more likely to find NURBS or other more sophisticated types of curves which require a bit more work to approximate with cubic segments.

On the 1d versus 2d issue -- From what I can see so far, After Effects uses one-dimensional piecewise functions for timing curves, although I don't have a copy to play with directly. However, poking at the implementation of Blender, it appears Blender f-curve segments do work similarly to cubic-bezier(), using (suitably constrained) 2d bezier curves to define the 1d function.

[visiblecode]

Additional observation: while you can muddle through with multiple keyframes and cubic-bezier() easings for most purposes, if you need smooth curves joined by a jump discontinuity, @keyframes as currently specified _can't_ be made to work. Best you can currently do to simulate such a jump discontinuity is to define two keyframes very close together and use a step easing between them:

@keyframes example {
    from {
        blah: 10px;
        animation-timing-function: cubic-bezier( ... stuff ... );
    }
    49.99999% {
        blah: 40px;
        animation-timing-function: step-end;
    }
    50% {
        blah: 100px;
        animation-timing-function: cubic-bezier( ... stuff ...);
    }
    to {
        blah: 150px;
    }
}

[birtles]

Best you can currently do to simulate such a jump discontinuity is to define two keyframes very close together and use a step easing between them

Yes, this is actually quite common to see. The Web Animations API allows you to overlap keyframe offsets so that you can add discontinuities and I believe there has been discussion in the past of adding syntax to allow you to do this in CSS keyframes (e.g. 50%+).

[visiblecode]

One suggestion made in the Slack discussion, which I had promised to document here, was to use an SVG path to specify an easing function.

In that case, any SVG path could be allowed, at least provided it ranged between 0 and 1 in the x dimension, and the curve's x component was continuous and monotonic over that range as well. In that case, the M operator could used to indicate jump discontinuities.

So, for two cubic segments joined by a jump discontinuity 50% of the way through, you might have something like: animation-timing-function: path("M 0,0 C 0.17,0.1, 0.33,0.2 0.5,0.4 M 0.5,0.8 C 0.67,0.8 0.83,0.9, 1,1")

I have mixed feelings about this, but it would work, aside from the issue of needing to indicate whether you wanted left- or right- continuity at any jumps.

[visiblecode]

The idea I had floated prior to that was something like: animation-timing-function: complex-easing(cubic(0, 0.1, 0.2, 0.4), 0.5, cubic(0.8, 0.8, 0.9, 1))

(In spite of cubic() having a superficial resemblance to cubic-bezier(), the parameters are all y values.)

i.e. two one-dimensional cubic bezier segments which meet at x = 0.5, but the first ends at y = 0.4, and the second begins at y = 0.8. Still doesn't address the issue of directional continuity though.

It does also require you to repeat the y/output value even when you want the two segments to join with C0 continuity. For example if the first segment ended at y = 0.4, and the second began there:

animation-timing-function: complex-easing(cubic(0, 0.1, 0.2, 0.4), 0.5, cubic(0.4, 0.8, 0.9, 1))

This also wouldn't allow for a direct translation of blender f-curves, while I think SVG paths would.

[rachelnabors]

This also wouldn't allow for a direct translation of blender f-curves, while I think SVG paths would.

That concerns me. Also, I can't imagine how to write a script to export to this format from a motion graph in, say, After Effects.

[visiblecode]

There's a meta issue here in that there's a bit of a mismatch between the way AE deals with animation and CSS to begin with. More specifically, animation-timing-function doesn't directly correspond to motion (v.s. timing) graphs in AE. It's more akin to the time remapping feature.

That being said, if you extract the x, y, etc. components from the motion separately (like the AE "separate dimensions" feature does), then you could turn them into separate animations with timing functions in the format I gave. But then CSS would need to provide a nice way to combine multiple transform: animations. (Today, you have to play tricks with nested divs.)

[birtles]

But then CSS would need to provide a nice way to combine multiple transform: animations. (Today, you have to play tricks with nested divs.)

We have that in CSS Animations 2: animation-composition

[grorg]

So if we ignore the composition and what-i-call-triggers-but-might-be-also-called-chaining, and assume spring() is handled separately (#280), and see @rachelnabors's recent tweet, can we start by adding some hardcoded shortcuts?

The majority of those on easings.net are variations of a cubic-bezier. If these are really useful, and if other implementors agree, we can add keywords for them.

Unless I've missed some, the functions on easings.net that are not supported by CSS are:

• easeInElastic
• easeOutElastic
• easeInOutElastic
• easeInBounce
• easeOutBounce
• easeInOutBounce

How popular are these? The first two are very much like spring().

Looking at tools...

After Effects only seems to have a couple of built-ins, which it calls "easy ease". However, it allows you to manually create some pretty complicated curves.

Apple's Motion does things in two different ways. It has "Behaviours" which are animation effects that you don't really see as keyframes and easing (more like "move in this direction with this speed and friction"). For the traditional keyframe animations, it has a manual editing mode like After Effects, but some shortcuts for bezier, linear, exponential, logarithmic and continuous.

Cinema 4D has basic ease in/out/both, linear and steps. It also has some tooling for smoothing keyframes (e.g. smooth tangents) which would likely produce curves that we couldn't exactly match in CSS at the moment.

Can people provide other examples?

[notoriousb1t]

@visiblecode. While I understand the hesitance to create an easing path function similar to SVG paths, I think it would make easings like GSAP's RoughEase.ease easier to do for tool makers.

http://greensock.com/ease-visualizer and click on Rough

[vidhill]

Hi,

I know there are two different types of animation being discussed in this, predetermined animation curves and programmatic animations, like Apple's spring.

I've been thinking about the latter and I think I have an idea.

What if we could facilitate scripted animation for transition values.

Here is the proposition I have arrived at..
I think it actually looks similar to how Houdini code will look, but I haven't delved deply into that as yes.

Anyway, your css would look something like this

.my-element {
    /* transition: transform 500ms url('../simple.js'); */
    transition: transform 500ms url('../bounce.js')(1 100 10 0);
    transform: translate(0px, 0px);
}

.my-element.active {
    transform: translate(200px, 200px);
}

Simple example of an ease function file

File: simple.js

/**
 * The simplest possible easing function, linear
 */
export init function(){
    //in this case init does nothing
}

/**
 * Function that gets called every frame until a done() callback / promise.resolve()
 * @param {float} t - Transition current Time, value from 0 to 1
 * @param {Promise} - Promise that gets resolved when animation is complete
 * @return {float} A value 0 is not transitioned at all and 1 is fully transitioned
 */
export frame function(t, animationComplete){
    if(t === 1){
        animationComplete.resolve('done');
    }    
    return t; // linear, very boring..
}

Example of how something more complex, e.g. Apple's bounce transition effect could be defined using this method

File: bounce.js

/**
 * Simulate a spring using the solving algorithm defined by this JavaScript
  function
 * @param {float} The mass of the object attached to the end of the spring. Must be greater
  than 0. Defaults to 1.
 * @param {integer} The spring stiffness coefficient. Must be greater than 0.
  Defaults to 100.
  * @param {integer} The initial velocity of the object attached to the spring.
  Defaults to 0, which represents an unmoving object..
  Defaults to 10.
   * @param {float} initialVelocity  
 */
export init function((mass, stiffness, damping, initialVelocity)){
    // code that need to be run once during initialization
    // -real code 
}

/**
 * Fuction that gets called every frame until a done() callback / promise.resolve()
 * @param {float} t - Time, value from 0 to 1
 * @param {promise} - Promise that gets resolved when animation is complete
 * @return {float} A value from 0 to 1+ where 0 is not transitioned at all and 1 is fully transitioned, in the case of spring the value overshoots 1 initially then eventually settles on 1 
 */
export frame function(t, animationComplete){
    // -real code
    // -real code
    return result;
}

The browser would know up front about the function and could, I assume be prepared,

Different variations of the spring, for example could be achieved by passing different values into the init function, which could be done from the CSS, no need to touch the js.

Obviously some code savvy people could share their functions with the community, and feasibly come up with some very clever stuff. And it would not need to go through the standards process, in the spirit of the Houdini project

The frame function would at maximum be executed every frame,
But of course the browser could decide to drop/skip frames if it needed,

The browser itself could work out how much rounding would happen.
The only thing the script could do is return a value 0-1 obviously overshooting 1 if the ease necessitated

[rachelnabors]

Interesting perspective, @vidhill. Thanks for sharing. I am personally a bit hesitant to wait to see how Houdini's adoption goes and what hiccups will come down the line when we could nail down a spec today. But if we can't, you very well may have described the future.

@grorg Thanks for joining the conversation! I'd love to see browsers offer more defaults than just ease-in, linear, etc. I was thinking adding easeOutQuint and the like. That's probably for another discussion, though, as we're chatting more about how to make a robust timing function that could underly other timing functions (like spring() and steps() ) and possibly be an export format for programs like After Effects. I've seen a real need from designers, as I know you have. What do you think?

[notoriousb1t]

It sounds good in theory, but I wonder if making a separate network call for each easing is a good idea. Even if you banked on HTTP2 to deliver it with the CSS file as an additional resource, it still would make CSS dependent on JS or a JS subset.

[vidhill]

@rachelnabors just to clarify this wouldn't be a proposal for something that would be necessarily be a part of the Houdini spec.
I doubt it would be necessary for Houdini to work out to implement this.

I mentioned Houdini because I imagine that it'd this would be preferable for it to align with the style/spirit.

@notoriousb1t I understand the concern, the first thing that comes to mind is the question, what if the user has js disabled!?
As this js would not be allowed to do any direct dom manipulation (or anything else), all it should do is return a number
Would a different rule be able to be applied to this js?

It shouldn't be capable of doing anything 'nasty'

[birtles]

There's a long-term plan to support script-defined timing functions but we're waiting on certain houdini components to materialize first. I think the current name of the piece we're missing is a worklet -- basically we want a bit of script that runs with very limited context and no side effects that we can run on either the main thread or compositor.

[vidhill]

@birtles I had a small chat about this on twitter with 'surma' and a few others,
I got some ideas on how I could re-do my example to be more inline with the Houdini conventions, and Surma recommended I send it in to the Houldini mailing list.

If this is already on the long term plans is the a point to doing this?
Would I be adding anything novel to the discussion?

-I'm new to the standards process, so genuinely don't know

[birtles]

@vidhill I think you should start a new issue for script-generated animations. This issue is pretty specifically about expanding the scope of timing functions that can be specified in a declarative manner. You could make that issue on this repository or on the web-animations one although I suspect it might be easier to start with Web Animations (since it is the lower level spec and already has a script API) and then we can layer CSS syntax on top later. In that issue, code examples using Houdini worklets would be useful.

[vidhill]

Thanks,
will do that, and I will update my code examples.

[vidhill]

@birtles I re-worked my proposition and posted it under the Houdini issues, https://github.com/w3c/css-houdini-drafts/issues/269

If you have any comments let me know.

[visiblecode]

@vidhill's proposal is pretty much the distilled essence of procedural animation. Using Javascript is great because you can directly specify any function you want. It's roughly what I'd personally want for most things. Main issue is the syntax; I think it'd be better if you could reference a Javascript function in the page context rather than having to use a separate .js resource.

That said, it's definitely a Houdini thing, for the reasons people have mentioned. One, it obviously requires Javascript to be available. And two, there has to be some guarantee that the animation function won't be poking at the DOM or network or global state. Neither is a problem in the context of Houdini, which assumes the availablity of JS to begin with, and has the "worklet" concept for isolating functions from the page's normal JS context. Houdini also should solve the "reference a fragment of JS from CSS somehow" problem in a general way.

[visiblecode]

But, that leaves us with the issue of what to do if you don't want to wait for Houdini, or rely on Javascript for stuff at this level. How do we let someone specify any timing function they could want without having to drop into Javascript?

Pretty much the only answer left after you rule out arbitrary code is to let authors define a timing function, piecewise, out of a sequence of simpler functions.

With that kind of representation hand authoring is out the window for anything that's not very simple, but browsers can provide more useful named presets to help with that. And if you're using an animation tool to export your CSS animations, you don't need to care.

How simple is simple? The simplest you can go is polynomials. We definitely need constant and linear segments, as well as curves.

Quadratic polynomials (i.e. ax² + bx + c) will cover those bases, though they're not very expressive. Also, for animation purposes, they're not so great because you can't use them to define piecewise curves with smooth acceleration.

Cubic polynomials (i.e. ax³ + bx² + cx + d) cover everything quadratic ones do, are a little more expressive, and allow smooth accelerations.

Quartic (ax⁴...) or quintic (ax⁵...) polynomials are even more expressive, but they also get wiggly and out of control very easily.

So, piecewise cubic polynomials end up being a kind of mathematical sweet spot for this purpose.

Unsurprisingly, this is how SVG paths work (if we ignore elliptical arc segments). If you boil down an SVG path, every segment in an SVG path amounts to a pair of cubic polynomials (or linear functions or quadratic polynomials which have a trivial conversion to cubics).

SVG paths use the bezier representation for polynomials (instead of an ax³ + bx² + cx + d kind of thing) because the bezier form, with control points, is more convenient for geometric purposes. Still equivalent underneath.

So, I'd say out of necessity we want something conceptually _like_ SVG paths, even if not exactly those. SVG paths allow some extra things like full-on gaps and overlaps which won't work for this purpose. (This stems from the 1d versus 2d issue I've talked about previously.) But you can restrict things, as with cubic-bezier().

The remaining thing you need to confront with using any kind of piecewise function for this purpose is how you deal with jump discontinuities. At the exact point where two segments butt up against each other, you need to be able to decide which one "wins". SVG doesn't care, it just draws at both positions. But for an animation timing function, you do need to pick one position or the other at the critical moment. (In CSS animation, steps() has to deal with this issue as well.)

[visiblecode]

So, to focus this a little more, roughly what we need is this:

• A way to define a timing function as a sequence of simpler functions, along with the breakpoints (as time in the 0 - 1 range) where one function hands off to the next.
• Probably using some kind of cubic bezier or quasi-bezier representation for the simple functions (could even literally be cubic-bezier(), at which point you might as well also allow any of the preset easings)
• With a way to specify which segment "wins" at a breakpoint between two segments (similar to "start" v.s. "end" with steps)
• That fits the spirit of existing CSS syntax

@keyframes is actually trying to accomplish roughly this, but it doesn't let you express jump discontinuities, it's building a whole animation rather than just a timing function, and it makes you explicitly calculate all the intermediate property values at every keyframe.

[visiblecode]

So, there are two ways forward:

1. fix @keyframes to allow jump discontinuities and let the browser calculate the property values for intermediate keyframes
2. introduce a new animation timing function syntax which lets you express a sequence of functions (maybe even just other timing functions) with the above characteristics

Either one should be sufficient for export from animation tools.

[notoriousb1t]

I think option 2 would provide a more obvious way to reuse timings with a transpiler and would make it accessible to css transitions.

[visiblecode]

So, how about something like this:

animation-timing-function: cubic-bezier(...), at 50% cubic-bezier(...), after 80% cubic-bezier(...);

(Using ellipsis so I don't need to think about inventing cubic-bezier parameters.)

The first cubic-bezier easing is time-scaled to the (0% to 50% time range), the second easing kicks in at exactly 50% time (and is time-scaled to the 50% to 80% time range), and the third easing kicks in just after 80% time (and is time-scaled to the 80% to 100% time range).

[visiblecode]

Actually that still doesn't adequately cover jump discontinuities. I'm forgetting that all the easing function outputs are constrained to be 0 at 0% and 1 at 100%, even though they're allowed to overshoot in between.

[visiblecode]

could do something like this (and show some stock easing functions in addition to cubic-bezier):

animation-timing-function: ease-out range(0, 0.3), at 50% ease-in range(0.3, 0.1), after 80% cubic-bezier(...) range(0.6, 1.0);

[notoriousb1t]

I need to test, but I think you can do steps(1,end) between two identical keyframes and it should stop animation for that time period.

[visiblecode]

the idea with range() is that it'd rescale the output of the simple timing function from 0.0 -> 1.0 to whatever you specify.

[visiblecode]

I should live up to my name for a change; here's a visual example.

Given:

animation-timing-function: ease-in range(0.0, 0.3), at 40% ease-out range(0.3, 0.1), after 70% cubic-bezier(... stuff ...) range(0.6, 1.0);

You'd get an animation timing function which graphs like this:

I think this accomplishes everything we've talked about wanting upthread.

[visiblecode]

The grammar would look something like:

<timing-function-segment> = <single-timing-function> [range(<number>, <number>)]?
<timing-function-segment-start> = [at | after]? <percentage>
<timing-function-extra-segment> =
    <timing-function-segment-start> <timing-function-segment>
<timing-function> =
    <timing-function-segment> [, <timing-function-extra-segment>#]?

If at/after is omitted before the percentage, at is assumed.

If range(...) is omitted, the segment's input (time) interval determines the output range.

[visiblecode]

The thing with range() being optional is mostly so you can keep using the existing syntax:

animation-timing-function: ease-in;

rather than having to explicitly write:

animation-timing-function: ease-in range(0.0, 1.0);

But it also means you can just chain a bunch of easings and get a continuous result, for example:

animation-timing-function: ease-in, 30% ease-in-out, 70% ease-out;

and get something equivalent to:

animation-timing-function: ease-in range(0.0, 0.3), 30% ease-in-out range(0.3, 0.7), 70% ease-out range(0.7, 1.0);

So it's actually not bad for hand-authoring in simple to medium cases.

[visiblecode]

(But the most important thing is still that tools should be able to reasonably export curves as a sequence of cubic-bezier() easings in this form.)

[visiblecode]

To clarify, since it's been asked -- at|after is determining where the previous segment ends and the new one begins along the horizontal axis. range() is determining the vertical range for a segment, and whether it's increasing or decreasing.

For very simple use cases (like backwards-compatibility with today's syntax), the two would sometimes be directly related (and range() becomes superfluous), but this wouldn't be the case in general.

[vidhill]

@visiblecode your train of thought all makes sense

[Martin-Pitt]

How does this look like when you have two or more animations and defining timing functions individually for each animation? Just checking that the comma syntax doesn't look too weird there, as it is usually used to separate different pairs/sets, e.g. like you can with multi background props.

[visiblecode]

@Martin-Pitt Ohh, that's a good point. Using commas in the syntax for a single (compound) easing function won't work, because it'd be ambiguous when used that way.

[visiblecode]

Let's say we strip down my original syntax proposal a little bit:

<timing-function-segment> = <single-timing-function> [<number> <number>]?
<timing-function-segment-end> = [until | through]? <percentage>
<timing-function-extra-segment> =
    <timing-function-segment-end> <timing-function-segment>
<complex-timing-function> =
    <timing-function-segment> <timing-function-extra-segment>*
<timing-function> = <complex-timing-function>#

This definition of <timing-function> is more compatible with the existing definition, which has used commas to support the multiple animation use case which @Martin-Pitt pointed out.

To reduce the verbosity a little, I've also replaced range() with a simple pair of numbers. "at" and "after" have also become "until" and "through", since without the commas it seems to read better if things are worded in terms of the end of the preceding segment instead of the start of the following one.

So with this syntax, my earlier example:

animation-timing-function: ease-in range(0.0, 0.3), at 40% ease-out range(0.3, 0.1), after 70% cubic-bezier(... stuff ...) range(0.6, 1.0);

would instead be:

animation-timing-function: ease-in 0.0 0.3 until 40% ease-out 0.3 0.1 through 70% cubic-bezier(... stuff ...) 0.6 1.0;

[visiblecode]

"until" is a little bit of a tricky word in English, because depending on context it may or may not be inclusive. (Here, I'm using "until" to mean an exclusive time bound for a segment, and "through" an inclusive one.) Would like some better suggestions for words, if anyone has ideas.

[visiblecode]

Also, if the output range is not given for a segment, it's probably better to default to using the starting/ending output values of the neighboring segments, if those are explicitly given. That would make hand-editing nicer.

If a neighboring segment doesn't have an explicit output range, or if there isn't a neighboring segment on one side, _then_ a segment can fall back to taking a starting/ending output value from its starting/ending percent time.

[grorg]

I'm jumping in late, but I'd like to point out that script-based timing functions should be limited to script-based animations (e.g. Web Animations).

The trick with animations, in particular CSS animations, is that the browser knows up front exactly what the animation is. This means it can easy do the animation in the compositing thread (or process), without impacting the main thread (UI). Script-based timing functions invalidate this opportunity, since there is no guarantee on the amount of time the function takes to compute. Yes, you can reduce the side-effects by putting the timing function in an isolated Houdini world, but that still doesn't stop an infinite loop.

This doesn't mean I'm against script-based timing functions (although I do think it in general it is more common to script the entire animation rather than just the timing function part). I just want to make it clear that a simple declarative time-bounded function is necessary, and probably solves 99% of use cases.

[rachelnabors]

I'm with @grorg on this one: simple, declarative, time-bound, a function to round out timing functions in the spirit of cubic-beziers, just with more flexibility for exporting and creating future declarative timing functions.

[birtles]

Just a few thoughts here:

• I don't know how important it is to worry about discontinuities here. It might be that it's sufficient to handle that using keyframes (assuming we'll eventually add a nicer syntax for overlapping keyframes such as 50%+ { ... }). Certainly if it complicates the syntax too much I'd suggest leaving it out.
• I like the idea of a 1d function. Solving the value for t before you can evaluate the function is a pain.
• Supporting SVG syntax sounds like overkill.
• The solution @visiblecode was moving towards seems very similar to this one here (item 4). Let's call it the chaining approach.
• The other major alternative being thrown around is one-big-function approach referenced (a) in the web animations spec, and (b) previously proposed to www-style by @AmeliaBR.
• We still do get a lot of requests for script-defined timing functions. I'm not sure if we will expose this to markup but I think in any case the proposal would be to time box them. (Also, talking about this over lunch with @shans, if we assume these functions are stateless, then we might not even need worklets for this since implementations could presumably just sample the function at, say, a ~100 points and just linearly interpolate between the points although that wouldn't work for discontinuities which I think the do want for script-defined timing functions.)
• Spring timing functions have the additional complication that you really would like the duration to be calculated from the springiness and distance of the animation. For this I think we can probably exploit the fact that the default animation duration in Web Animations is "auto" but I believe Google might not have another proposal for this.

[birtles]

Moving this to [css-timing-2] since I believe that is where we will end up addressing this.

[AmeliaBR]

previously proposed to www-style by @AmeliaBR.

I'd kind of forgotten about that. I'd definitely forgotten that I'd made nice figures to go with it. It would probably be helpful if they were copied over here. Pulling out the key points from my August 2015 proposal here, with some updated links.

---

Make the definition of cubic Bézier curves:

A cubic Bézier curve is defined by a series of control points, P0 through Pn (see [the figure] for an example where n=4). P0 and Pn are always set to (0,0) and (1,1), respectively. The parameters to the easing function are used to specify the values for points P1 to Pn-1. These can be set to preset values using the keywords listed below, or can be set to specific values using the cubic-bezier() function. In the cubic-bezier() function, each point Pi is specified by both an X and Y value.

Then farther down, the syntax and definition of the cubic-bezier function is replaced as follows:

 cubic-bezier([<number>, <number>]*)

Specifies a cubic-polybezier curve. Each pair of values specifies a point Pi in the form x1,y1; an odd-numbered sequence of values is invalid. All x values must be in the range [0, 1] and each x value must be equal to or greater than the previous; otherwise, the definition is invalid. The y values are unrestricted.
The series of points is converted to a series of connected cubic Bézier curve segments by grouping into sets of three: two control points followed by a vertex point. If the number of points (plus the implicit 1,1 end point) is not a multiple of three, the sequence is padded with the point 1,1 to create complete cubic Bézier segments.

For example,

• A cubic-bezier function with no parameters is equal to cubic-bezier(1,1, 1,1), which is essentially a linear timing function.
• The ease-in function could also be written as cubic-bezier(0.42,0).
• A multiple bounce transition could be written as follows, resulting in the curve visualized in [Figure]:

     cubic-bezier(0.25,0.25, 0.25,0.75, 0.3,1,
                  0.5,0.5, 0.6,0.5, 0.7,1,
                  0.85,0.8 0.9,0.8)

Finally, a new function could be added to make it easier to make smooth curves:

smooth-cubic-bezier([, ]*)
Specifies a cubic-polybezier curve with automatically-calculated smooth connections between segments. Each pair of values specifies a point Pi in the form (x1, y1); an odd-numbered sequence of values is invalid. All x values must be in the range [0, 1], each x value must be equal to or greater than the previous; otherwise, the definition is invalid. The y values are unrestricted.

If there are 1 or 2 pairs of values provided, the result is the same as for the cubic-bezier function. For 3 or more points, an implicit control point is inserted after every vertex point, that is equal to that vertex point plus the vector from the previous control point to that vector point. The remaining explicit points therefore alternate between control points and vertex points. Again, the sequence of points is padded with 1,1 if necessary to make complete cubic Bézier segments.

For example, the following two functions specify the same curve:

smooth-cubic-bezier(0,0.75, 0,1, 0.5,0.5)
cubic-bezier(0,0.75, 0,1, 0.5,0.5, 1,0, 1,1)

Both result in the curve visualized in [Figure]

A first approximation at the figures are attached; if you want to play around quickly, you can also fork from https://jsfiddle.net/L1o71c1c/1/ Or, you know, write a script to generate the SVG markup automatically from a function specification.

Things to discuss:

Given these definitions, should new pre-defined functions be introduced to represent bounce/elastic timing functions in popular JS libraries?

Is the restriction on x values appropriate? We need to ensure that the final curve is a proper function, with each x value having a single corresponding y value. Forcing vertex and control points to be in sorted x order should ensure this, but may be overly restrictive.

It is nonetheless possible to draw a completely vertical arc segment with the current wording. We could address this by adding another restriction (the x values for vertex points must be strictly greater, not just greater or equal to) or we could add an interpretation rule (apply the maximum value, consistent with how the steps function works).

Are the commas between every number in the cubic-bezier function necessary? Do current implementations enforce that syntax? Compare with (a) the Shapes spec which requires commas between points in a polygon, but does not allow them between x y pairs, and (b) SVG syntax, which allows commas and whitespace interchangeably, so many people with mathematical background use commas to join x y pairs and whitespace to separate them, like x1,y1 x2,y2.

[Note that there were comments on the proposal at the time from [Brian Birtles](https://lists.w3.org/Archives/Public/public-fx/2015JulSep/0038.html), including a link to an even older proposal, that I'll copy into a separate comment to get everything in one place.]

[AmeliaBR]

Proposal for "Stacked Timing Functions" from (I think) a face-to-face breakout session in May 2015, as sent to the fx mailing list in June 2015 by @birtles.

---

STACKED TIMING FUNCTIONS

• Stacked timing functions would allow you to emulate the effect of
  nested groups.
• However, Brian points out that chained timing functions have the same
  ability to emulate arbitrary easings, and are also more accessible and
  more widely applicable - e.g. to produce spring-like easings.

We worked on a syntax for chained timing functions and came up with:

easing: [ tf? point? ]?

Concretely, easings look like

easing: cubic-bezier(a,b,c,d) (x, y) cubic-bezier(e,f,g,h) (x2,y2) ...

You can leave out the points (they're evenly distributed between
provided points, where easings always start at (0,0) and end at (1,1).

You can leave out the timing functions (in which case they'll default to
linear).

cubic-bezier parameters are always in global (0,0,1,1)-space. This means
that you can accidentally provide erroneous easings, e.g.:

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) (0.5, 0.3) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

Here the first point has an x coordinate that is less than the second
x control point of the first bezier (0.5 < 0.6). Concretely, an easing
is OK as long as all of the x coordinates (specified and inferred) are
in nondescending== increasing order.

So this is incorrect too, although it's hard to see why:

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

becomes:

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) (0.5,0.5) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

(because that's what easing: linear linear would do)

We could instead infer point x coordinates to be evenly spaced between
adjacent specified x coordinates, which would mean that the above would
be equivalent to

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) (0.6,0.5) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

which is actually fine. But if we're doing that, should we do the same
thing for the y coordinate?

easing: cubic-bezier(0.2, 0.8, 0.6, 0.6) (0.6,0.75) cubic-bezier( 0.6, 0.9, 0.7, 1.0)

Google to polyfill this. If it's good then we'll add something to L2.

[argyleink]

moving comments from #3838 to here. looks like what I'd specified and more has been covered in this thread, but I'll share what I'd said anyway.

Why

Physics aren't likely to land any time soon to help folks with spring, bounce or cliff effects, and there's big demand for these engaging and lifelike animation tactics. Due to lacking phsyics, folks bring in javascript animation libraries to do the work, or visit websites that generate 100s of keyframes, or just flat out abuse the cubic-bezier() function. JS libraries and cubic-bezier() abuse being the most common, since it's the easiest.

Most of these workarounds result in difficult to manage, rigid or uncanny animations that don't make the web look very great at animation.

Examples

cubic-bezier()
https://codepen.io/AdrienBachmann/pen/VYVvGo

JS library (34kb)
https://codepen.io/rossorthwein/pen/XorVVV

Proposal

I think we could pacify the need for physics by adding the ability for cubic-bezier() to take more points. Extend cubic-bezier() to chain/concat points together.

Current

Proposed
Where we currently have 2 pairs passed into cubic-bezier(), we allow passing additional pairs so more points could be created.

Explode out:


source

.animated-layer {
  transition: .2s cubic-bezier(.17,.67,.83,.67,.2,.02,.73,.59, ...);
}

[ghost]

Howdy,

A potential approach mentioned earlier in this thread was using SVG paths to describe complex ease curves. A blocker to this approach was that tooling would have to be created to export this kind of path data from programs such as After Effects.

I had this exact same problem a few years ago, and made an After Effects script which does just that: https://github.com/SupportClass/ae-ease-to-gsap-customease

It's not perfect, but it shows that this route has some validity. Although this script has not been updated in some time, I still use it frequently and can verify that it still works.

Hopefully this is useful, and apologies if this route of exploration was already closed. I tried to follow the thread the best I could before posting, but definitely feel like I missed some nuance.

[argyleink]

I'm feeling partial to @AmeliaBR's proposal of smooth-cubic-bezier() as well as adding additional pre-defined functions for things like bounce and elasticity. Cool work! It would be nice to get rid of the commas as well, good call.

[AmeliaBR]

@Lange, that is helpful.

What would also be helpful is a write-up of what values / options are supported (or not) in the major animation software that support complex custom easing curves. Anyone have good resources for that?

Looking at the Adobe help pages for After Effects, it looks like the complex easing can be a mix of smooth or sharp changes, or even steps.

So I'm now starting to doubt whether it is enough to swap between smooth and full beziers for the entire sequence. Maybe it make more sense to focus on chaining arbitrary segments. Making a syntax easy to write by hand is good. But it's probably more important to ensure that it can accurately represent easings that are already being used in design tools.

I like @vidhill's suggestion of trying to define the easing using a syntax that defines the progress as a direct function of time, instead of a syntax that defines an arbitrary 2D curve and then tries to constrain it to only having one progress value for each time point. But the question again is: can existing software export to the syntax without loosing information?

[SebastianZ]

As @visiblecode mentioned earlier, we could simply reuse the path() function currently defined in the Motion Path Module and referring to SVG paths.

That allows combinations of straight lines, quadratic and cubic Beziérs, gaps, and more, in short, should cover all use cases and is consistent to what we already have.

Btw., the timing functions were generalized to also cover color gradients and therefore were renamed to "easing functions". I assume, everything discussed here also applies to gradients, so, maybe someone could rename the summary of this issue accordingly?

Sebastian

[AmeliaBR]

@SebastianZ
Path syntax is certainly the most expressive, but it requires extra work to calculate a y-value (interpolated value) at a given x value (time progress or position). And there is no guarantee that you'd get a single y value for any x value.

And yes, we are now talking about generic interpolation functions (although the use cases here all seem to be animation), so I've updated the title to refer to the current name of the spec.

[SebastianZ]

... it requires extra work to calculate a y-value (interpolated value) at a given x value (time progress or position).

Can you please elaborate on that? I don't see why that's work than multiple Beziérs.

And there is no guarantee that you'd get a single y value for any x value.

Right, same issue for Beziérs.

I see two solutions for this problem:

1. Invalidate those paths or Beziérs as you mentioned earlier.
2. Clamp the x coordinate so that the path always increases in x direction. This possibly manipulates the path but makes all paths or Beziérs valid.

Visualisation for the latter:

Input path:

Normalized path:

Sebastian

[visiblecode]

That sort of normalization is pretty rough to pull off in a robust/understandable/easy to implement way.

The big issue we're up against here is that cubic beziers (and SVG paths) aren't really suited for defining easing functions, because they treat x and y _independently_.

This is good for drawing 2d shapes that are supposed to be able to overlap themselves in arbitrary ways. But for reasons that are pretty obvious above this is super awkward for applications where y is supposed to _depend_ on x, like for easing functions.

Honestly the ideal tool for this is something like a cubic hermite spline. Apart from being about as simple as you can get from an implementation perspective, they're friendlier to hand authoring than beziers are going to be. You'd just need to supplement them with a way to indicate instantaneous jumps in position/speed.

[visiblecode]

Let's look at that in practical terms. To define a cubic hermite spline, you just need a list of (x, y, y') triples.

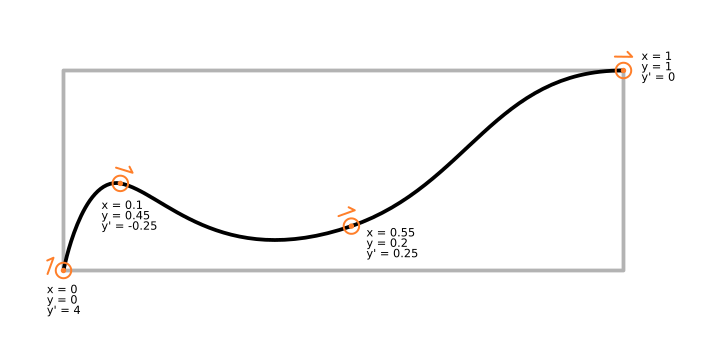
In this context, x would be time, y position, and y' speed. Which should make some intuitive sense from an animation point of view.

[visiblecode]

Right there, that's enough to do most any kind of motion, including springy animations etc. The missing piece is animations where speed or position change abruptly.

So, for the impact point in bounce animations you have to be able to give the incoming and outgoing speed separately.

Animations with jumps in position are similar-ish, except you also need to say which of the incoming or outgoing position gets used when the time is exactly x.

So, without getting too much into syntax, this means you might have a choice of four keyframe/control point "types" for easing splines:

• smooth - (x, y, y')
• sudden speed change - (x, y, y'_in, y'_out)
• sudden position change, use incoming position - (x, y_in, y'_in, y_out, y'_out)
• sudden position change, use outgoing position - (x, y_in, y'_in, y_out, y'_out)

Seems decent for hand-authoring, and it's also general enough to support export from most animation software, either exactly or as an extremely close approximation.

[visiblecode]

Also worth adding that segments of cubic splines are easy to convert into Bernstein form, so implementors can re-use code they already have around for evaluating Beziers.

[tabatkins]

Note that step easings have already made a decision of whether the moment of transition uses prev or next value: they use the next value. So presumably we'd be consistent there, as the use-case for making it controllable seems extremely minimal - you'd only see the difference if you purposely advanced a paused animation to exactly that progress %.

---

Overall, uh, that sounds like a pretty good idea, and the fact that the curve is automatically c1-continuous is nice (unless you purposely drop to c0- or non-continuous by providing additional arguments). I like the physicality of being able to provide a velocity directly, which enables realistic-looking bounces really easily by just inverting the y velocity, like your example shows. (Versus chained beziers, which require much more guess-and-checking to get a realistic-looking bounce.)

[visiblecode]

I think I can sweeten the pot a bit more for hand-authoring. Let's say there's also an auto option for velocity that picks a velocity for you.

For a smooth node with neighbors on both sides, auto would mean choose the velocity to get _C2_ continuity. That way, if you wanted you could spell out just the times and positions by hand, and automatically get buttery smooth motion.

In the remaining situations, auto would pick the velocity assuming no acceleration. That gives you an easy shorthand for linear motion, which would otherwise be a little clunky to do by hand.

[AmeliaBR]

I do like @visiblecode's proposal for hand-authoring friendliness (especially with an automatic curve fitting option), and for the fact that it directly defines y as a function of x, so doesn't need arbitrary limits or fix-ups.

But hand-authoring is only half of the argument. The other is compatibility with existing tools.

Also worth adding that segments of cubic splines are easy to convert into Bernstein form, so implementors can re-use code they already have around for evaluating Béziers.

Do you have a link to the relevant formulae? Are these exact conversions or approximations?

Ideally, this would become the new "master" syntax, that could represent all the keyword and function-notation easings defined in the current spec. In particular, I'd be interested to know if your definition of "automatic" velocity calculations matched Blender's automatic handles.

But we'd also want to directly represent curves that can be generated in popular animation software, like AfterEffects and Blender, which seem to use a mix of straight lines and cubic curves (with internally-enforced limits on the curves to keep them always increasing in the x direction).

We'd also want to make it possible to convert from software that currently uses path notation, like Greensock. Which, based on my testing with their visualizer, seems to use the rule proposed by @SebastianZ to convert arbitrary paths into functions.

[visiblecode]

My take-away from the couple years I spent on this is:

1. There's too much variation in the way different software represents animation curves to allow for a "master" representation that can seamlessly roundtrip with all of them
2. Some popular ways of specifying animation curves only allow approximate implementations to begin with
3. Where round-tripping the original representation isn't a concern, any animation curve can be converted to cubic splines with good fidelity (sometimes with added control points)

[visiblecode]

brief overview on the math, I can go into more detail on specific things if you want

Every segment of a cubic spline translates to a cubic polynomial. There are a number of ways to represent a cubic polynomial, which are all exactly convertible (within the limits of floating point precision etc.), including:

• the obvious way: ax³ + bx² + cx + d
• Hermite form: starting value, starting tangent, ending tangent, ending value
• Bernstein form: starting value, two control values, ending value

The thing is, Bézier curves are based on Bernstein polynomials (the bezier handles map to the control values). The catch is that a 2D Bézier curve segment consists of two polynomials, one for x and one for y. For drawing curves on screen that's perfect, the two polynomials can be evaluated directly, independently, with all the usual advantages of cubics. Mathematically precise, versatile, and efficient to evaluate.

But, for uses like CSS's cubic-bezier(), you have to solve for the unique root of the x polynomial (with things constrained so there is one), and plug the result into the y polynomial. The root finding part isn't possible to do super efficiently, so in practice what most implementations of cubic-bezier() do is precompute a rough approximation and linearly interpolate over that. It works _okay_, but there's a big speed/accuracy tradeoff. Probably there's more variation between implementations than people realize, especially in extreme cases.

TBH, in general implementors would probably get better results (both in terms of accuracy and also performance) converting each cubic-bezier() segment to a cubic spline (of ~1-3 segments) rather than trying to approximate cubic-bezier() directly in realtime.

There are a bunch of other animation curve representations which get used as well, NURBS and so on. Some of these superficially resemble Béziers (they have similar handles, etc.), but don't allow exact conversion to/from them.

Blender's smoothing is a bit different to the auto thing I described above (which is based on spline interpolation). Blender's curves can still be approximated by cubic splines but you wouldn't use auto to do it.

[visiblecode]

We'd also want to make it possible to convert from software that currently uses path notation, like Greensock. Which, based on my testing with their visualizer, seems to use the rule proposed by @SebastianZ to convert arbitrary paths into functions.

What Greensock does is discard the parts of the path between where x starts decreasing to where it catches up again. I don't know the details of the implementation, but bezier path intersections tend to have rough edge cases to account for.

Obviously any reasonable easing representation should be able to support export of a "baked" representation (_after_ pruning, etc). But should browsers be expected to implement on-the-fly pruning themselves?

[AmeliaBR]

But should browsers be expected to implement on-the-fly pruning themselves?

If we adopt a system where you can directly use SVG path notation, then yes, I would expect some sort of reasonable error handling like that. So that comment was more of an aside, going back to the discussion of the alternative.

But if we adopt something like the cubic spline syntax, the main question is can a tool like Greensock implement an algorithm to convert (with a reasonable degree of fidelity) their fixed-up path into the standard notation.

[flackr]

I have on occasion found myself wanting to supply a formula to express timing functions for example when I wanted to perfectly invert another timing function to implement an accelerated expanding reveal animation. We ended up approximating this inverse scale with a generated linear animation with lots of keyframes but it could have been expressed as a single formula. Could supplying a formula solve some of these other express-ability use cases as well?

[visiblecode]

@AmeliaBR wrote:

If we adopt a system where you can directly use SVG path notation, then yes, I would expect some sort of reasonable error handling like that.

Fair!

But if we adopt something like the cubic spline syntax, the main question is can a tool like Greensock implement an algorithm to convert (with a reasonable degree of fidelity) their fixed-up path into the standard notation.

Yes.

@flackr wrote:

We ended up approximating this inverse scale with a generated linear animation with lots of keyframes but it could have been expressed as a single formula. Could supplying a formula solve some of these other express-ability use cases as well?

Mostly no. (Though having calc() available as an _option_ for easing functions is kind of tempting anyhow.) The problem is many functions don't have a (practical) formula representation -- _including functions that result from cubic-bezier()'s (ab)use of Béziers!_

The simplest general-purpose solution for representing arbitrary functions (including ones that can't be expressed as formulas) is to use a piecewise polynomial approximation.

Piecewise linear (degree 1) is one version of that, but as you discovered needs a lot of keyframes.

Piecewise cubic (degree 3), which we're discussing here, is kind of a sweet spot where you don't need that many extra keyframes, but it's still cheap to evaluate and can't go uncontrollably wiggly as can be a problem for degree >= 4.

[visiblecode]

But if we adopt something like the cubic spline syntax, the main question is can a tool like Greensock implement an algorithm to convert (with a reasonable degree of fidelity) their fixed-up path into the standard notation.

Apparently this isn't a requirement for Greensock. I chatted with the Greensock author about this today, and the way he explained it was instead of generating CSS and delegating to the browser, Greensock always drives animations from JavaScript.

Greensock has its own internal representation for easings that's optimized for efficiency vs perfect accuracy, and it always converts everything (CSS-style easings, SVG path easings, etc) to that internal representation before animating.

[visiblecode]

Probably exporting animations from Blender is a better model use case.

[visiblecode]

I had a thought this week -- knots in a spline are a lot like stops in a gradient, just
with value+slope instead of colors.

...what if the syntax for splines worked like the syntax for gradients?

animation-timing-function: cubic-spline(<position> <speed> <time%>, ...);

So for example:

animation-timing-function: cubic-spline(0 0 0%, 0.1 auto 25%, 0.5 auto 50%, 0.9 auto 75%, 1 0 100%);

It probably makes sense to support some shorthands.

To start with, using the rules for gradient stops, if you just want equal spacing you can leave off the knot times/percentages:

animation-timing-function: cubic-spline(0 0, 0.1 auto, 0.5 auto, 0.9 auto, 1 0);

It'd probably also make sense to make speed optional (defaulting to auto):

animation-timing-function: cubic-spline(0 0, 0.1, 0.5, 0.9, 1 0);

(Both of these give the same result as the original above.)

That feels pretty nice.

If we go with the same rules as for gradients, you can create abrupt changes by doubling up knots:

animation-timing-function: cubic-spline(0, 1 50%, 1 50%, 0);

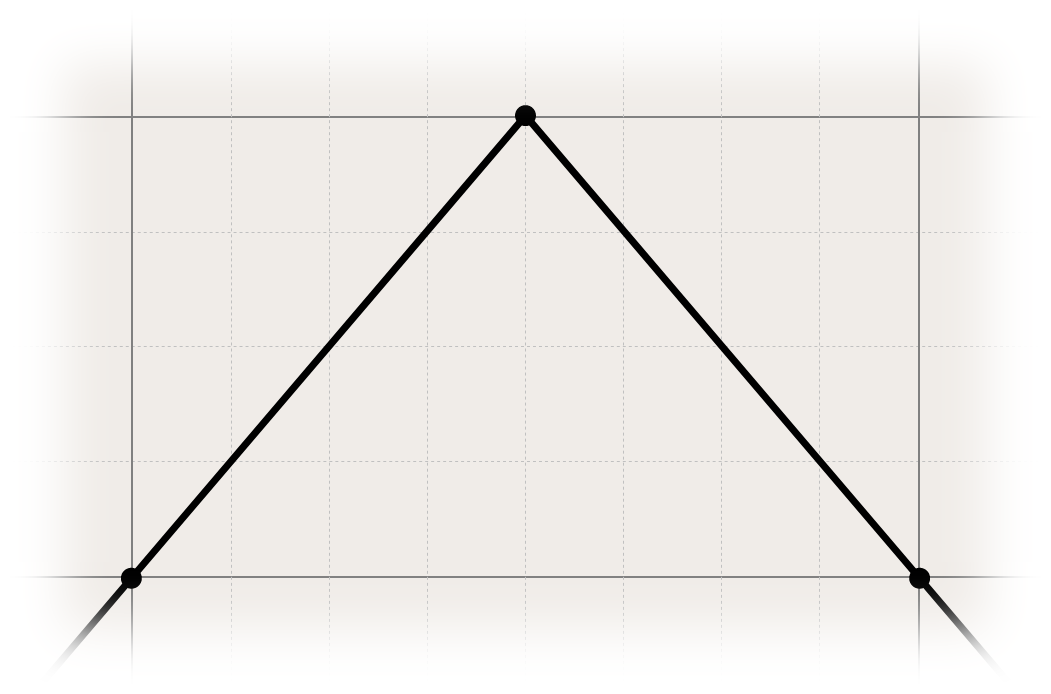
animation-timing-function: cubic-spline(0.5, 1 50%, 0 50%, 0.5);

animation-timing-function: cubic-spline(1 0, 0 -3 50%, 0 3 50%, 1 0);

EBNF syntax for this idea might look something like:

<cubic-spline-easing-function> = cubic-spline( <cubic-spline-knot-list> )

<cubic-spline-knot-list> = <cubic-spline-knot> [, <cubic-spline-knot># ]?
<cubic-spline-knot> = <cubic-spline-knot-position> <cubic-spline-knot-speed>? <cubic-spline-knot-time>?

<cubic-spline-knot-position> = <number>
<cubic-spline-knot-speed> = auto | <number>
<cubic-spline-knot-time> = <percentage>

[visiblecode]

Also, here's a bounce easing I prepared by hand:

animation-timing-function: cubic-spline(0 0, 1 50%, 1 50%, 0.5, 1 75%, 1 75%, 0.75, 1 87.5%, 1 87.5%, 0.875, 1 93.75%, 1 93.75%, 0.9375, 1 96.8%, 1 96.8%, 0.968, 1 98.4%, 1 98.4%, 1);

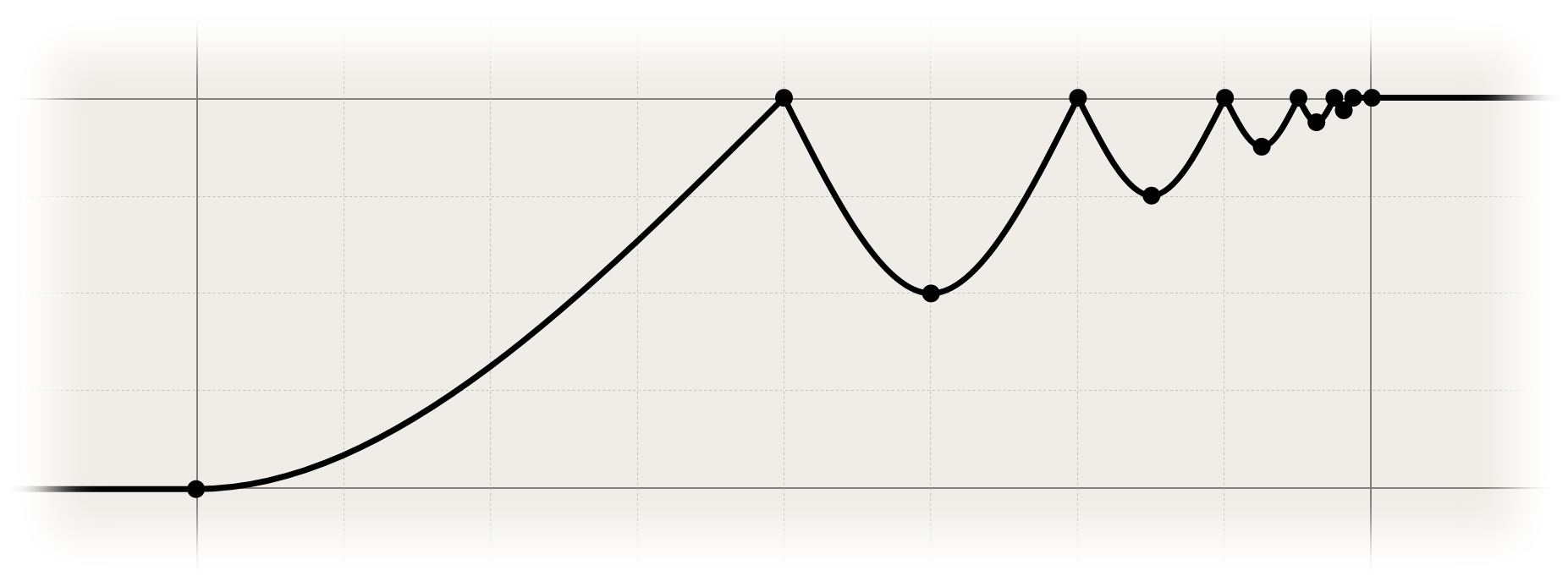
Edit: Also, a handmade spring easing.

animation-timing-function: cubic-spline(0 0, 1.5 0 50%, 0.75 0 75%, 1.125 0 87.5%, 0.9375 0 93.75%, 1.031 0 96.8%, 0.984 0 98.4%, 1 0);

[birtles]

Those are neat diagrams and the effects you've produced look great. They seem to cover the different use cases well.

As someone who is not very familiar with gradients (I need to look it up every time) I don't find the parallel with gradient syntax particularly helpful. In particular, putting the "y" value (<cubic-spline-knot-position>) before the "x" offset (<cubic-spline-knot-time>) feels back-to-front compared to how I'm used to thinking with regards to keyframe offsets. However, that may be just me, and given that these easing functions may be used with gradients, aligning the syntax probably makes sense.

Currently all easing functions go from (0,0) to (1,1). I'm unsure if we should break that invariant or not (as this syntax currently allows). I seem to recall it had unfortunate implications in the realm of GroupEffects (where timing functions are effectively layered on top of one another) but perhaps it's ok.

[visiblecode]

Since it's already allowed in a more limited way, letting the dependent variable (progress) to go outside the 0..1 range shouldn't be much of a problem.

For the independent variable (time), though -- I'd imagined we'd just use the section of the timing function between 0 and 100%, regardless of where the first/final knots are, extrapolating past the end knots with straight lines if necessary.

animation-timing-function: cubic-spline(0 0 30%, 1 0 66%);

[visiblecode]

I'm not super attached to the gradient syntax, it just seemed like a nice opportunity for syntactic uniformity with the rest of CSS.

[birtles]

Since it's already allowed in a more limited way, letting the dependent variable (progress) to go outside the 0..1 range shouldn't be much of a problem.

Right, that part is fine.

For the independent variable (time), though -- I'd imagined we'd just use the section of the timing function between 0 and 100%, regardless of where the first/final knots are, extrapolating past the end knots with straight lines if necessary.

What I'm more concerned about is when f(0) != 0 or f(1) != 1. There certainly used to be places where we assumed that. With step-start you can already have f(0) != 0 but only when the "before flag" is false.

I recall that in the past that invariant proved useful but perhaps it's fine now. (It may have been when we were trying to chain timing functions together, or when we were trying to invert them in order to work out when to dispatch events -- but we don't do either of those things anymore).

[visiblecode]

What I'm more concerned about is when f(0) != 0 or f(1) != 1. There certainly used to be places where we assumed that. With step-start you can already have f(0) != 0 but only when the "before flag" is false.

I recall that in the past that invariant proved useful but perhaps it's fine now. (It may have been when we were trying to chain timing functions together, or when we were trying to invert them in order to work out when to dispatch events -- but we don't do either of those things anymore).

It'd be worth grounding out on whether there are any lingering issues with lifting this restriction, for both Gecko and WebKit. As long as the restriction is in place, there's a whole family of complex animations left that can't be expressed except the "long way", with multiple keyframes.

For example:

Without the requirement that f(0) == 0 and f(1) == 1, this animation could be expressed the same way as other complex animations (using the gradient-style strawman syntax):

@keyframes bouncy {
    0% {
        transform: translate(0px);
        animation-timing-function: cubic-spline(0, 1, 0 33%, 0 33%, 0.33, 0 66%, 0 66%, 0.11, 0);
    }
    100% {
        transform: translate(90px);
    }
}

But, if the restriction were in force, for certain animations like this one you'd be forced to fall back to something like:

@keyframes bouncy {
    0% {
        transform: translate(0px);
        animation-timing-function: cubic-spline(0, 1 0);
    }
    16% {
        transform: translate(90px);
        animation-timing-function: cubic-spline(0 0, 1);
    }
    33% {
        transform: translate(0px);
        animation-timing-function: cubic-spline(0, 1 0);
    }
    49% {
        transform: translate(30px);
        animation-timing-function: cubic-spline(0 0, 1);
    }
    66% {
        transform: translate(0px);
        animation-timing-function: cubic-spline(0, 1 0);
    }
    82% {
        transform: translate(10px);
        animation-timing-function: cubic-spline(0 0, 1);
    }
    100% {
        transform: translate(0px);
    }
}

(There's still a somewhat shorter way to write this, which I'll leave as an exercise for the reader because it requires a re-parameterization that's annoying to do by hand.)

[AmeliaBR]

@visiblecode How would you handle transitions, or filled animations, if the easing function doesn't reach the the target “end” value at the end time? Would the value jump suddenly to match?

[visiblecode]

@visiblecode How would you handle transitions, or filled animations, if the easing function doesn't reach the the target “end” value at the end time? Would the value jump suddenly to match?

Yes, similar to the current situation with some step easings.

Edit: For fills, I guess it might make sense to hold the last computed value to make animations like the above possible. Which would be different to the behavior for step.

[birtles]

Edit: For fills, I guess it might make sense to hold the last computed value to make animations like the above possible. Which would be different to the behavior for step.

Right, for fills it is already possible to fill at the mid-point of an interval by using animation-iteration-count: 0.5 for example.

[visiblecode]

That's an interesting point. I think we can get away without having any special fill behavior.

For use cases involving complex exported animations, multiple intermediate keyframes would be the norm anyhow.

[css-meeting-bot]

The CSS Working Group just discussed easing timing functions.

The full IRC log of that discussion

<fremy> Topic: easing timing functions

<astearns> github: https://github.com/w3c/csswg-drafts/issues/229

<fremy> AmeliaBR: this is another old issue, that had a lot of discussion for a while, but every so often somebody finds it again, and revives the issue

<fremy> AmeliaBR: the issue is that all the easing functions are only continuous curves

<fremy> AmeliaBR: you can use strong coefficients to create a slight overshoot, but that doesn't allow rebounds

<fremy> AmeliaBR: so the request is to have more complex functions

<fremy> AmeliaBR: most animation software have ways to create those functions, but now they can't be exported to css

<hober> q+

<fremy> AmeliaBR: and they have to be exported to huge keyframe sequences which are difficult to maintain and understand

<hober> https://lists.w3.org/Archives/Public/www-style/2016Jun/0181.html

<astearns> https://github.com/w3c/csswg-drafts/issues/229#issuecomment-492367598

<fremy> AmeliaBR: there is a proposal to use cubic bezier but it allows too much for what we want

<fremy> AmeliaBR: there is also a more recent proposal, and I happen to like it

<dbaron> cubic beziers as defined currently are well-defined functions since we give only 2 of the 4 control points and the x values are constrained to [0,1]

<fremy> AmeliaBR: but there is also the option of using the cubic bezier syntax and let the browser fix that up if the function isn't pure

<astearns> ack hober

<fremy> AmeliaBR: so our first question, what should we do first, get a great syntax or extend the type of syntax we have now

<hober> spring(mass stiffness damping initialVelocity)

<fremy> hober: we think this is a good idea

<fremy> hober: we like this syntax, and we are all for it

<fremy> astearns: any other comment?

<fremy> heycam: what's the unit that this proposal used?

<fremy> heycam: css values should have the answer

<flackr> q+

<fremy> astearns: dbaron pointed out on irc that cubic-bezier can work as functions

<astearns> ack flackr

<fremy> AmeliaBR: yes because we remove some parameters, but as you try to add expressivity, it's difficult to maintain that

<majidvp> q+

<astearns> ack majidvp

<fremy> majidvp: one thing I like about this idea, it's possible to approximate a spring using the proposal, which is great because other we have to specify ourselves all the types of bounds we want, but authors will still want more

<hober> s/we think this is a good idea/dean proposed a spring timing function a few years ago. we're supportive of having such a thing./

<fremy> AmeliaBR: yes, if we have a generic expression syntax that handles many things, we can get spring to be an alias to that

<hober> s/we like this syntax, and we are all for it//

<argyle> 😍

<fremy> astearns: I don't see much desire to discuss the precise syntax, but there is some interest

<fremy> fantasai: should we add somebody to edit the spec?

<fremy> astearns: but I don't see enough interest to add this to a spec

<fremy> myles_: AmeliaBR what are you trying to achieve here?

<fremy> AmeliaBR: get agreement that a generic mechanism would be great to add to easing-2

<fremy> myles_: my problem with the generic approach, is that the end result is just complex math, and doesn't explain what the end result should look like

<fremy> myles_: which is why I prefer spring because it has clear intent

<fremy> myles_: also, as designer, I think I would draw what I want in a software, as a piece-wise function

<astearns> ack dbaron

<fremy> myles_: and that is not easy to express as a cubic-bezier

<fremy> dbaron: I think adding new things in that space is reasonable, but I think I would want to weight the implementation cost, but in general I'm in favor of adding expessivity in the spec here

<fremy> AmeliaBR: the last proposal has very nice pictures, and seem well accepted

<dbaron> dbaron: nice pictures and few/no equations

<fremy> astearns: one way to make progress is to find the contributor that submitted the various comments, and convince that person to collect them in a spec in wicg

<fremy> AmeliaBR: I'm willing to try to get that to happen, if there are other people interested they are welcome to join me

<majidvp> q+

<fremy> flackr: I'm interested in the space as well, but didn't evaluate

<fremy> flackr: the current proposal

<astearns> ack majidvp

<fremy> flackr: but my attention will be about ease of write, and ease of parse

<fremy> fantasai: and ease-of-read as well

<fremy> flackr: yes

<fremy> majidvp: i would also want to note that if you have an houdini approach, we can allow any js function, then sample it

<fremy> majidvp: previously houdini was a big leap in the space

<fremy> majidvp: but right now, we have a lot of things ready, and this would be easily doable

<fremy> hober: I'm weary of putting off very desirable features to js

<fremy> majidvp: I'm not saying we shouldn't do a declarative approach, but I don't see why both can't be pursued at the same time

<fremy> hober: sure

<fremy> myles_: we are fine with a houdini approach

<fremy> myles_: but that shouldn't prevent us from delivering features that are directly relevant to authors

<hober> s/to js/until houdini is ready/

<myles_> s/we are fine with a houdini approach/the presence of houdini doesn't allow us to stop making good features for our users/

<majidvp> I agree with that sentiment :)

<fremy> AmeliaBR: ok, so the conclusion is that we are going to try to gather a community to make this happen, thanks everyone for the feedback

<fremy> <br /> (after which we would talk about motion-blur)

[visiblecode]

dbaron: nice pictures and few/no equations

I wasn't sure if spelling out the equations would be necessary at this stage. As mentioned upthread, the piecewise curves here are supposed to be Cubic Hermite splines. They are a standard thing and very closely related to Bezier curves.

Hermite splines can be given as a sequence of (_t_, _p_, _m_) triples, corresponding to the knots. In this context those correspond to (_time_, _progress_, _velocity_), with _time_ and _progress_ ranging between 0 and 1, apart from under/overshoot.

(n.b. the strawman CSS syntax from earlier gives _t_ last, and as a percentage, just because it's trying to imitate CSS gradient syntax.)

I'll use _t₀_ to mean the _t_ from the first knot, _t₁_ from the second knot, and so on...

For evaluating the curve in between knots, it's probably easiest to convert the segments to Bernstein form. (Bezier curves are made of polynomials in Bernstein form.)

Converting one Hermite segment, between knots _n_ and _n+1_, to Bernstein form and re-parameterizing for the unit interval:

Δt_n = t_n+1 - t_n

C₀ = p_n
C₁ = p_n + m_n * Δt_n / 3
C₂ = p_n+1 - m_n+1 * Δt_n / 3
C₃ = p_n+1

Evaluating the converted segment for some _t_, using De Casteljau's algorithm, as is commonly done for Beziers:

lerp(a, b, x) = (1 - x) * a + x * b

t_unit = (t - t_n) / Δt_n

B₀ = lerp(C₀, C₁, t_unit)
B₁ = lerp(C₁, C₂, t_unit)
B₂ = lerp(C₂, C₃, t_unit)

A₀ = lerp(B₀, B₁, t_unit)
A₁ = lerp(B₁, B₂, t_unit)

result = lerp(A₀, A₁, t_unit)

One non-standard thing is that I'm allowing zero length segments (where _t_n_ == _t_n+1_) to represent abrupt changes in the curve; these trivial segments shouldn't get evaluated.

When I have a chance, I'll follow up on how to compute unspecified _m_n_ values (missing or auto in the strawman syntax).

[visiblecode]

Missing _m_n_ values (slopes) can be worked out by solving a system of linear equations with an equation per knot.

If a knot's slope is already known, the equation is trivial:

m_n = the slope

Otherwise, assuming:

Δt_n = t_n+1 - t_n
Δp_n = p_n+1 - p_n

It's a choice between:

A. m_n = 0
B. 2 * m_n / Δt_n + m_n+1 / Δt_n = 3 * Δp_n / Δt_n²
C. m_n-1 / Δt_n-1 + 2 * m_n / Δt_n-1 = 3 * Δp_n-1 / Δt_n-1²
D. m_n-1 / Δt_n-1 + 2 * m_n * (1 / Δt_n-1 + 1 / Δt_n) + m_n+1 / Δt_n = 3 * (Δp_n-1 / Δt_n-1² + Δp_n / Δt_n²)

Which equation to use depends on the knot's neighbors:

| Previous Knot | Next Knot | Equation |
| --- | --- | --- |
| none | none | A |
| none | same _t_ | A |
| same _t_ | none | A |
| none | different _t_ | B |
| same _t_ | different _t_ | B |
| different _t_ | none | C |
| different _t_ | same _t_ | C |
| different _t_ | different _t_ | D |

This choice of equations amounts to doing standard spline interpolation for each unbroken section of curve with unknown slopes.

The tridiagonal matrix algorithm is a good fit for solving the resulting system of equations and is easy to implement.

[AmeliaBR]

Thanks for the equations, @visiblecode !

What did you think about turning this into a WICG proposal? That would have two benefits:

1. People would be able to edit and keep track of the final proposal without reading this entire thread!
2. It would involve you confirming that you're contributing all your intellectual property claims in your proposal under a licence that is compatible with W3C specs.

Myself and @argyleink have said we'd be able to help coordinate & deal with the formatting aspects of the proposal, but we'd need the IP contributions sorted out first.

[visiblecode]

Okay, I'm willing to give it a shot, though it may be a couple weeks before I can get back to you.

[argyleink]

wanted to share for potential reference and relevance https://github.com/lunelson/split-ease